План урока:

Уравнения с двумя переменными

График уравнения

Линейные уравнения с двумя переменными

Системы линейных уравнений

Системы с тремя переменными

 

Уравнения с двумя переменными

В 5 уроке мы уже изучили понятие уравнения. Под ним подразумевается любое равенство, которое содержит переменную величину. Напомним, что переменная величина – это, по сути, буква в выражении, вместо которой можно подставлять произвольные числа.

Если в равенстве находятся две переменные величины, которые обозначаются разными буквами, то оно считается уравнением с двумя переменными (или двумя неизвестными).

Можно привести несколько примеров подобных уравнений:

x + y = 9

8ds + d² = 0

4h = 6k

Если в уравнение

x² + 2y = 6

подставить х = 2 и у = 1, то оно обратится в справедливое равенство:

2² + 2*1 = 6

Поэтому пару действительных чисел (2;1) называют решением этого уравнения.

При записи (2;1) важно условиться, к какой переменной относиться первое число в скобках, а к какой – второе. Обычно, если в уравнении в качестве переменных применяют х и у, то сначала указывают значение х, а после – значение у.

Очень часто у уравнений имеется бесконечное множество решений, хотя у некоторых из них их может и не быть. С уравнениями с 2 неизвестными можно делать те же преобразования, что и с иными равенствами, а именно:

1. переносить слагаемые через знак «=», меняя при этом их знак на противоположный;
2. умножать и делить обе части равенства на число,либо выражение, которое, не должно равняться нулю;
3. выполнять тождественные преобразования, такие как раскрытие скобок, разложение многочлена на множители, приведение подобных слагаемых и т.п.

Эти преобразования называются равносильными (или тождественными), так как при их использовании множество решений уравнения остается неизменным.

Ещё раз обратим внимание на выражение

x² + 2y = 6

Перенесем слагаемое x² вправо, добавив ему знак минус:

2y = 6 - x²

Далее поделим равенство на 2:

y = 3 - 0.5x²

 

Получили новое уравнение, которое равносильно исходному. Однако с его помощью значительно проще искать решения уравнения. Достаточно выбрать любое значение х, после чего можно определить и вторую переменную. Например:

если x = 0, то y = 3-0.5*0² = 3

если x = 1, то y = 3-0.5*1² = 3 - 0.5 = 2.5

если x = 4, то y = 3-0.5*4² = 3 - 8 = -5

Все эти пары (0; 3), (1; 2,5), (4; – 5) являются решениями исходного уравнения.

Перейдя с помощью равносильных преобразований к равенству

y = 3 - 0.5x²

мы получили, по сути, функцию переменной у от х. Математики говорят, что величина у выражена через величину х.

Пример. Выразите переменную m из равенства

 

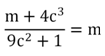
Решение.

Так как m присутствует в обеих частях равенства, необходимо выполнить тождественные преобразования. Сначала избавимся от дроби. По свойству операции деления делимое равно произведению делителя и частного, поэтому можно записать:

m + 4c³ = m(9c² + 1)

Раскроем скобки справа:

m + 4c³ = 9c²m + m

Теперь перенесем слагаемые 9c²m и m влево с противоположным знаком, а 4c³ – вправо:

m - 9c²m - m = -4c³

Теперь в правой части не осталось буквы m. Осталось убрать лишние символы из левой части. Для этого сократим подобные слагаемые:

-9c²m = -4c³

Теперь поделим обе части на (– 9c²):

m = 4c/9

В результате нам удалось получить выражение для величины m.

График уравнения

Любое действительное число можно отметить на координатной прямой, а пару чисел – на координатной плоскости. Если же нанести на плоскость все возможные решения, то получим какую-то линию, которую принято считать графиком уравнения.

Для построения графика можно с помощью тождественных преобразований свести уравнение к функции, а потом построить график этой функции.

 

Рассмотрим это на примере следующего уравнения:

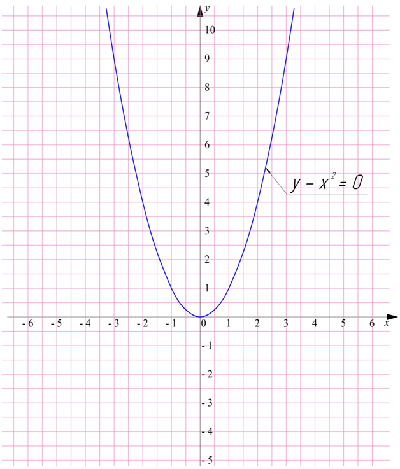
y - x² = 0

Попытаемся выразить у через х.

Для этого перенесем в уравнении слагаемое (– x²) вправо:

y = x²

Получили степенную функцию, чей график нам известен. Он представляет собой параболу (см. урок Функции) График исходного уравнения выглядит также:

Однако график функции и график уравнения – это разные понятия. Дело в том, что ряд уравнений невозможно свести к функции. Например, для равенства

x² + y² = 25

Однако график функции и график уравнения – это разные понятия. Дело в том, что ряд уравнений невозможно свести к функции. Например, для равенства

0 + y² = 25

Решая его, получаем два корня

y² = 25

y = -5 и y = 5

В результате мы нашли две точки для графика, (0; 5) и (0; – 5).

 

Теперь подставим другое значение х, например, х = 3:

3² + y² = 25

y² = 16

y = -4 и y = 4

Нашли ещё 2 точки: (3; 4) и (3; – 4)

 

Далее примем х = 4, получим уравнение:

4² + y² = 25

y² = 9

y = -3 и y = 3

таким образом нашли точки (4; – 3) и (4; 3).

Аналогичным образом, подставляя вместо х числа 5, – 5, – 4, – 3, можно найти точки (5; 0), (– 5; 0), (– 4; 3), (– 4; – 3), (– 3; 4) и (– 3; – 4). Отметим их все и соединим плавной линией:

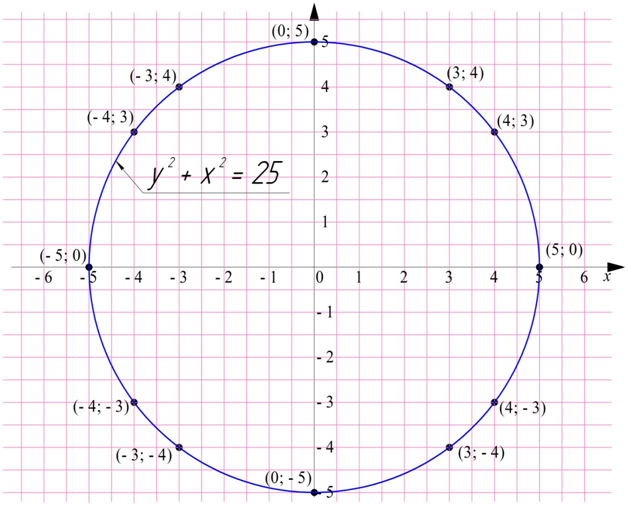
График выглядит как окружность (Позднее, в 10 классе, будет строго доказано, что это именно окружность).

Окружность не может являться графиком функции, так как одному значению x должно соответствовать единственное значение у. Однако на рисунке видно, что для х = 0 подходит два значения у: 5 и – 5.

Линейные уравнения с двумя переменными

Запишем несколько похожих друг на друга уравнений:

5x + 6y = 7

-1.56x + 2.17 = 87.57

4x - 11y = -12

Всех их объединяет то, что они представимы в виде

ax + by = c

где а, b и c– это какие-то произвольные числа (константы, или коэффициенты). Подобные уравнения называют линейными уравнениями с двумя переменными.

Для обозначения числа c используется термин «свободный член».

Линейные уравнения так называют из-за того, что их график – это прямая линия. Дело в том, что они легко сводятся к линейной функции.

 

Пример. Постройте график линейного уравнения с двумя переменными

-4x + 2y = 6

Решение.

Попытаемся выразить у через х, чтобы получить какую-то функцию. Чтобы слева осталось только выражение с у, перенесем одночлен (– 4x) вправо:

2y = 4x + 6

Теперь необходимо избавиться от двойки слева, чтобы получить выражение для у, поэтому поделим равенство на 2:

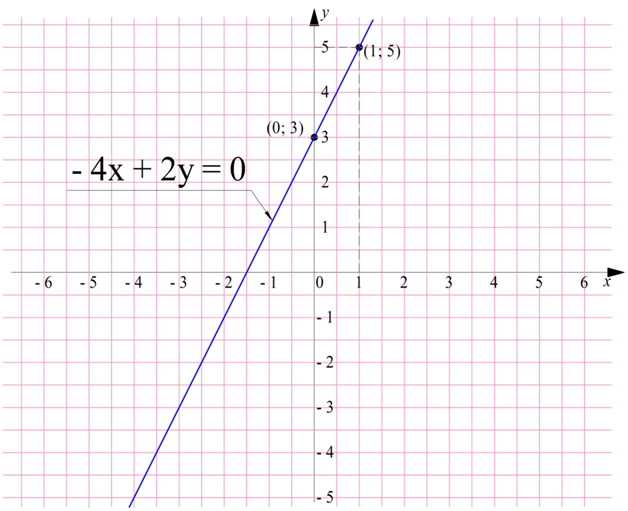
y = 2x + 3

Это линейная функция. Чтобы построить ее график, достаточно найти координаты двух ее точек:

при x = 0 н = 2*0 + 3 = 3

при x = 1 y = 2*1 + 3 = 5

Получили точки (0; 3) и (1; 5). Отмечаем их на координатной плоскости и соединяем прямой:

 

Отдельно рассмотрим несколько частных случаев.

Если нулю равен коэффициент при x, то получаем уравнение

0x + by = c

откуда получаем

by = c

y = c/b

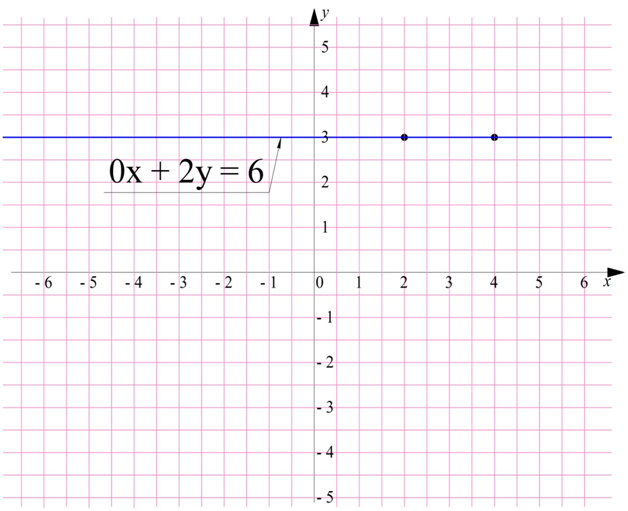
Получается, что при любом значении х величина у остается неизменной и равной дроби b/c. Из предыдущего урока мы знаем, что графиком таких функций является горизонтальная линия.Убедимся в этом на примере уравнения

0x + 2y = 3

Подставим в него, например, х = 2, получим

0*2 + 2y = 6

2y = 6

y = 3

Получили точку (2; 3).

Теперь подставим х = 4

0*4 + 2y = 6

2y = 6

y = 3

Получили точку с координатами (4; 3)

Видно, что при подставлении любого х в уравнение оно умножается на ноль, и остается равенство

2y = 6

Соединим две найденные точки прямой, она окажется горизонтальной:

Если же нулю равен коэффициент при у, получаем уравнение

ax + 0y = c

откуда получаем

ac = c

c = c/a

При любом значении у величина х не меняется, поэтому графиком уравнения будет вертикальная линия.

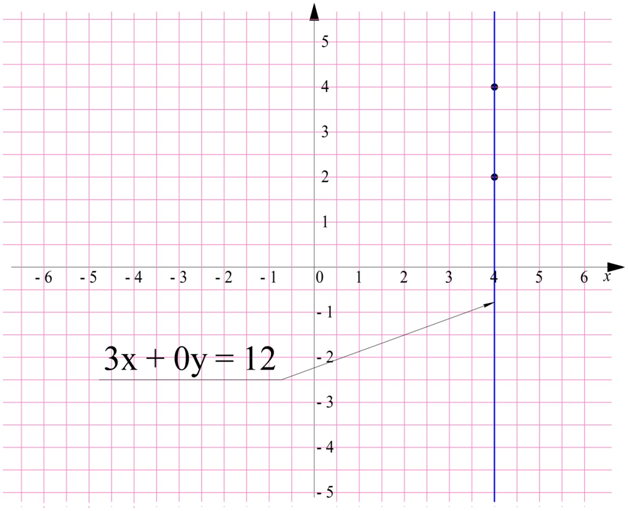
Убедимся в этом на примере уравнения

3x + 0y = 12

Подставляя у = 2, получим равенство

3x + 0*2 = 12

3x = 12

x = 4

Имеем точку с координатами (4; 2)

Теперь возьмем другое значение у, например, 4. Тогда получаем:

3x + 0*4 = 12

3x = 12

x = 4

Получили еще одну точку (4; 4). Видно, что какое бы значение х мы не подставляли в уравнение, в итоге всегда получается равенство

3x = 12

Имеющее единственное решение

x = 4

поэтому у всех точек графика абсцисса будет равна 4. Отметим найденные две точки и соединим их прямой, она оказывается вертикальной:

Когда обе константы при переменных равны нулю, то возможны два случая. Если свободный член также нулевой, то получаем равенство

0*x + 0*y = 0

Оно, очевидно, справедливо вообще для всех значений переменных, поэтому его график – вся координатная плоскость.

Примером случая, когда свободный член не равен нулю, является

0*x + 0*y = 1

Понятно, что графиком этого уравнения является пустое множество, так как оно не имеет ни одного решения. Поэтому нарисовать график уравнения не получится.

Системы линейных уравнений

В младших классах мы изучали задачи, которые требовали для своего решения записи всего одного уравнения. Однако порою условия формулируются так, что для их описания на языке математики удобно использовать две переменные и 2 уравнения.

 

Пусть требуется найти такие два числа, чья разность равна четырем, а сумма двум.

Обозначим первое число за х, а второе за у. В сумме они дают двойку, это можно записать следующим образом:

x + y = 2

Их разность равна 4, что описывается так:

x - y = 4

Получили два линейных уравнения. Оба имеют бесконечное количество решений. Однако нам нужно общее решение, которое одновременно будет подходить для обоих равенств. В таком случае математики говорят, что следует решить систему линейных уравнений.

Для формального обозначения системы применяют фигурные скобки:

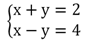
Очень наглядным является графическое решение системы уравнений. Покажем его на примере этой задачи. Для этого построим графики для обоих уравнений, из которых состоит система.

Преобразуем первое уравнение системы, выразив из него у:

x + y = 2

y = 2 - x

Получили линейную функцию, для построения графика которой достаточно 2 точек:

при x = 0, y = 2 - 0 = 2

при x = 1, y = 2 - 1 = 1

Имеем 2 точки: (0; 2) и (1; 1)

Аналогично преобразуем и второе равенство:

x - y = 4

-y = -x + 4

y = x - 4

Также найдем две точки для этого уравнения:

при x = 0, y = 0 - 4 = -4

при x = 1, y = 1 - 4 = -3

Нашли точки (0; – 4) и (1; – 3). По найденным точкам можно построить графики обоих уравнений:

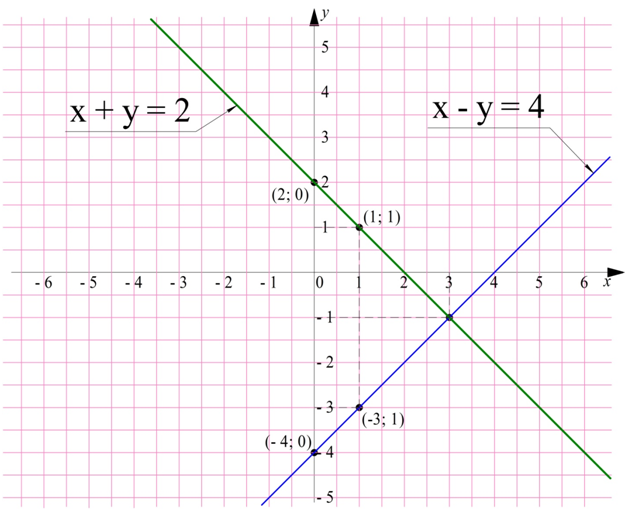
На рисунке видно, что два графика пересекаются в точке (3; – 1), поэтому именно эта пара чисел является решением системы. В этом можно убедиться с помощью подстановки чисел.

Графики очень удобны для анализа количества решений системы (в том числе состоящей и из нелинейных уравнений). Ясно, что любые две прямые на плоскости

• либо пересекаются в одной точке;
• либо параллельны друг другу;
• либо совпадают.

Соответственно, система из двух линейных уравнений с двумя неизвестными может иметь

• ровно 1 решение;
• ни одного решения (если графики параллельны друг другу);
• бесконечное количество решений (если графики совпадают).

Графики двух линейных функций параллельны, если у них совпадают угловые коэффициенты,но различаются свободные коэффициенты. Если же оба коэффициента совпадают, то графики совпадают.

 

Пример. Найдите, сколько решений есть у системы

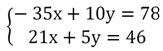
Решение. Преобразуем каждое равенство, чтобы выразить у:

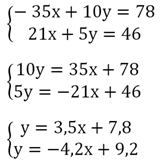
Полученные линейные функции различаются своими угловыми коэффициентами (напомним, что угловые коэффициенты у линейной функции – это числа перед переменной х, в данном случае они равны 3,5 и (– 4,2)). Их графики пересекаются, а значит, исходная система имеет ровно 1 решение.

 

Пример. Сколько пар чисел удовлетворяют условию

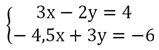
Решение.

Выразим у через переменную х:

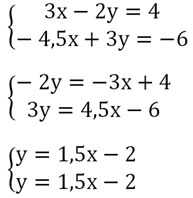
С помощью тождественных преобразований мы получили из каждого уравнения одну и ту же линейную функцию. Их графики совпадают, а потому у системы бесконечное количество решений.

Конечно, графический способ решения систем уравнения часто дает лишь приближенное значение, ведь рисунки невозможно всегда выполнить абсолютно точно. Да и рисовать график под каждую задачу довольно неудобно, а компьютерная техника производит вычисления с числами, а не картинками. Поэтому удобно использовать иные, аналитические методы решения линейных уравнений, которые не требуют построения графиков уравнений. Один из них называется способом подстановки. Отметим сразу, что он является весьма универсальным и может использоваться для систем, содержащих и более 2 переменных, а также состоящих и из нелинейных уравнений.

В чем заключается его суть? Сначала над одним из уравнений производят тождественные преобразования, чтобы, в конце концов, выразить одну из переменных. После этого полученным выражением заменяют эту переменную в других уравнениях. В результате выраженную переменную удается исключить, что упрощает решение системы. Рассмотрим это на примере.

 

Пусть есть система

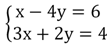
Преобразуем 1-ое равенство, перенеся слагаемое (– 4y) вправо:

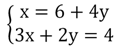
Мы смогли выразить x через y. Теперь можно осуществить подстановку в 1-ое равенство:

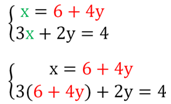
Итак, в первое равенство мы подставили его выражение для величины х, полученное из второго равенства. В результате этой операции нам удалось получить уравнение с одной переменной:

3(6 + 4y) + 2y = 4

Подобное мы уже умеем решать:

3(6 + 4y) + 2y = 4

18 + 12y + 2y = 4

14y = 4 - 18

14y = -14

y = -1

Найдя значение одной величины, можно вернуться к выражению для х:

x = 6 + 4y

Подставим в него у = – 1 (это действие называют обратной подстановкой):

x = 6 + 4*(-1) = 6 - 4 = 2

Итак, мы нашли решение (2; –1).

Опишем алгоритм использования метода подстановки, который состоит из 4 шагов:

1. Выражаем одну из неизвестных величин, используя какое-нибудь исходное уравнение.
2. Далее заменяем выраженную величину во втором равенстве на выражение, полученное на 1-ом шаге.Получим новое уравнение, содержащее лишь одно неизвестное.
3. Решаем новое уравнение и тем самым находим значение одной неизвестной.
4. Делаем обратную подстановку и находим значение второй неизвестной.

Стоит отметить, что неважно, какую неизвестную и через какое уравнение выражать. Это лишь вопрос удобства вычислений. В конечном итоге ответ получится один и тот же

Пример. Найдите решение системы способом подстановки:

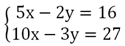
Решение.

Будем выражать у через 1-ое равенство:

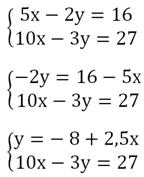
Далее выражение для у подставим во второе уравнение:

10x - 3(-8 + 2.5x) = 27

10x + 24 - 7.5x = 27

2.5x = 27 - 24

2.5x = 3

x = 1.2

Далее выполним обратную подстановку:

y = -8 + 2.5x = -8 + 2.5*1.2 = -8 + 3 = -5

Ответ (1,2; – 5).

Для систем, состоящих из линейных уравнений, очень удобен другой метод, который называют способом сложения.

Его суть заключается в том, что если два равенства верны, то можно сложить отдельно их правые и левые части и получить новое верное равенство. Например, есть равенства

8*5 = 40

3*4 = 12

Они верны. Сложим их и получим

8*5 + 3*4 = 52

И это тоже верное равенство.

Такие же действия можно совершать и с уравнениями, входящими в одну систему. Пусть дана система

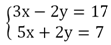
Произведем сложение:

(3x - 2y) + (5x + 2y) = 17 + 7

3x - 2y + 5x + 2y = 24

8x = 24

x = 3

Получилось, что при сложении левых частей сократились слагаемые 2y и (– 2y). Это произошло из-за того, что коэффициенты при этих слагаемых являются противоположными числами.

Найдя x, подставим его в любое из исходных уравнений, например, в первое, и решим его

3x - 2y = 17

3*3 - 2y = 17

-2y = 17 - 9

- 2y = 8

y = -4

Получили решение (3; – 4).

 

Что же делать, если в системе нет переменной, у которой в разных уравнениях стоят противоположные коэффициенты? В таком случае нужно умножить одно из равенств на какое-нибудь число, чтобы создать удобную для сложения ситуацию.

 

Пример. Решите систему способом сложения:

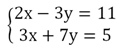
Решение. Умножим первое равенство на (– 3), а второе на 2:

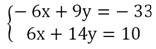
Теперь перед x стоят противоположные коэффициенты, а потому можно произвести сложение:

(-6x + 9y) + (6x + 14y) = -33 + 10

-6x + 9y + 6x + 14y = -23

23y = -23

y = -1

Теперь подставим полученное значение y в первое равенство:

2x - 3y = 11

2x - 3*(-1) = 11

2x = 8

x = 4

Ответ: (4; – 1).

Системы с тремя переменными

До сих пор мы рассматривали способы решения систем линейных уравнений, в которых фигурировало только 2 неизвестные величины. Однако на практике встречаются и системы уравнений с тремя переменными.

Для их решения можно использовать и способ подстановки, и способ сложения. А вот графический метод здесь уже не поможет. Дело в том, что каждая точка на координатной плоскости представляет собой пару чисел, например, (5; 0), (4; 7) или (– 3; 2). Также и решение систем с двумя неизвестными является парой чисел, что позволяет использовать точки на плоскости для обозначения этих решений. Но решением системы с 3 неизвестными является не пара, а уже тройка чисел, а ее отметить как точку на плоскости не получится.

Рассмотрим задачу. Периметр треугольника равен 30 см. Первая сторона больше второй на 4 см, а удвоенная длина третьей стороны равна сумме первых двух сторон. Необходимо найти каждую из сторон треугольника.

Обозначим стороны треугольника как a, b и c. Задача представляет собой набор трех условий, для каждого из которых можно сформулировать отдельное уравнение:

a + b + c = 30 (периметр оставляет 30 см)

a = b + 4 (1-ая сторона больше 2-ой на 4 см)

2c = a + b (сумма двух сторон равна удвоенной 3-ей стороне)

В результате получаем систему

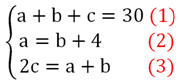
Рядом с каждым равенством мы поставили числа (1), (2) и (3). Это делается для удобства записи решения, чтобы можно было ссылаться на выражения. Подобные обозначения часто используются в научной литературе.

Будем решать уравнения способом подстановки. Видно, что в (2) уже выражена переменная a. Подставим (2) в (3):

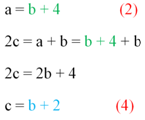
Нам удалось выразить и переменную c. Теперь подставим (2) и (4) в (1):

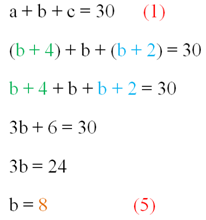
В результате нам удалось найти одну из сторон, которую мы принимали за переменную b. Она равна 8 см.

Теперь подставим (5) в (2) то есть выполним обратную подстановку:

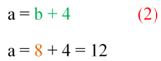
Нашли, что вторая сторона треугольника составляет 12 см.

Далее подставим (5) в (4)

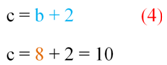
Третья сторона оказалась равной 10 см.

В результате получили, что стороны треугольника равны 12, 10 и 8 см. Аналогично решаются системы линейных уравнений с любым количеством переменных. Заметим лишь, что для того, чтобы система имела единственное решение, количество уравнений в ней не должно быть меньше количества переменных. Существуют универсальные алгоритмы (самым известным из них является метод Жордана-Гаусса), позволяющие с помощью компьютера решать системы с тысячами и даже миллионами переменных. Такие задачи могут возникать при расчете прочностей различных строений и деталей машин, моделировании процессов переноса тепла, течения жидкости, протекания электрического тока. Так, на рисунках показаны результаты моделирования столкновения двух автомобилей, а также расчет аэродинамики гоночной машины:

Расчет прочности автомобилей при столкновении 

Моделирование воздушных потоков, обтекающих автомобиль