Математика

Сложение и вычитание дробей
План урока:
Сложение дробей с разными знаменателями
Вычитание дробей с разными знаменателями
Сравнение дробей с разными знаменателями
Мила очень любит домашних животных, именно поэтому, у неё дома живут два замечательных котенка - Рик и Мик. Девочка самостоятельно ухаживает за котятами, балует своих любимцев. Но когда она уходит в школу за питомцами присматривает мама. Сегодня Мила вернулась со школы и увидела на столе записку от мамы: « Доченька, я покормила котят. Рику досталось две пятых банки корма, а Мике три четвертых. Может кто-то из них остался голодным – дай добавки». Мила заволновалась, как понять, кому досталось больше, а кого еще нужно покормить? Девочка вспомнила, что сегодня на уроке математики они решали похожие задания, но Мила была занята своим смартфоном и не особо разбиралась в изучаемой теме.
На помощь пришла бабушка, она что- то быстро написала на тетрадном листочке и сказала внучке, что по её расчетам Рик скушал 15/20 корма, а его друг всего 8/20. Поэтому добавки нужно дать Мику. Вот тут Мила и поняла, как важно уметь складывать дроби с разными знаменателями.
Сложение дробей с разными знаменателями
Например:
В бассейне установлена новая система фильтрации. За один час первая труба наполняет бассейн на одну четвертую часть, а вторая труба на одну шестую. Какая часть бассейна будет заполнена водой, если в течение одного часа одновременно будут работать обе трубы?

Чтобы ответить на главный вопрос задачи нам нужно суммировать части заполнения бассейна, при одновременной работе обеих труб. Получается, нам необходимо суммировать одну четвертую и одну шестую. Стоит обратить внимание, на то, что цифры, стоящие под чертой отличаются. Возникает вопрос «Как сложить дроби с разными знаменателями?».
Для решения заданий такого типа, в математике применяют специальный порядок действий.

Учитывая рассмотренный порядок, вычислим сумму:
- Определим НОЗ для одной четвертой и одной шестой. Для этого четыре и шесть представим в виде составляющих:

Сейчас, определим число, на которое нужно умножить каждую составляющую математического выражения. Для этого, вычислим частное найденного НОЗ и четырех, а после – шести:
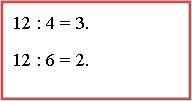
Значит, оба компонента в записи одна четвертая, будем умножать на три, а обе составляющие записи одна шестая на два. Вспоминаем, как привести дробей к общему знаменателю:

Получается,
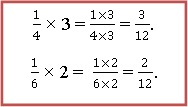
Теперь можно суммировать найденные выражения с одинаковыми цифрами под числителем, этим действием мы узнаем, на сколько заполнится водой резервуар. Применим определение:

Выполняем:

В случае одновременной работы двух труб, за один час наполнится водой бассейна.
Вычитание дробей с разными знаменателями
Разберем ситуацию:
На стройке первый каменщик выложил камнем три восьмых фундамента дома, второй работник сделал на одну девятую меньше, чем первый. Какую часть фундамента выложил камнем второй каменщик?

На первый взгляд задача очень простая. Чтобы ответить на главный вопрос, необходимо найти разность двух данных значений. Но известные дробные выражения имеют разные цифры, находящиеся под числителем. Как же вычитать дроби с разными знаменателями?
Для выполнения заданий такого типа, применяется определенный алгоритм:

Для проведения вычислительных операций, применим изученное правило.
Для начала, определим НОЗ для одной девятой и трех восьмых.Для этого разложим числа девять и восемь на компоненты:

В полученных разложениях повторяющихся составляющих нет. Следовательно, находим произведение всех имеющихся чисел:

Далее, определим число, на которое нужно умножить каждую запись. Для этого разделим найденный НОЗ на цифру, стоящую внизу первой, а потом второй дроби:
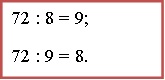
Умножим оба компонента в записи три восьмых на девять, а компоненты в записи одна девятая на восемь:
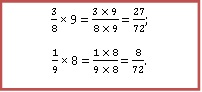
Мы преобразили данные числа, и выяснили, что один работник сделал двадцать семь семьдесят вторых всей работы,а другой – неизвестно, на восемь семьдесят вторых меньше. Нужно выяснить, какую долю всего объема работы сделал второй рабочий. Ответить на данный вопрос можно с помощью вычитания. Вспоминаем правило:

Учитывая рассмотренное определение, найдем разность:
дроби надо прописать
Получается, второй каменщик выложил камнем 19/72 всего фундамента.
Мы рассмотрели, как правильно выполнить сложение и вычитание дробей с разными числовыми значениями, находящимися под дробной чертой. А как же сравнить две дроби, имеющие разные числа, стоящие под числителем?
Сравнение дробей с разными знаменателями
Выполним задание
Сравните 7/25 и 8/20.
Полученное задание, моментально ставит в тупик. Сразу возникает вопрос «Как выполнить сравнение дробей, ведь знаменатели разные?». Арифметика предусмотрела такие вопросы и приготовила правило, запомнив, которое можно выполнять любые сравнения:




Сложение смешанных чисел
Разберем ситуацию.
Для заготовки одной банки консервированных овощей нужно взять 1 килограмма огурцов и 1 килограмма помидоров. Сколько всего килограммов овощей нужно подготовить для консервирования одной банки овощей?

Чтобы ответить на главный вопрос задачи, нам следует найти общую массу огурцов и помидоров. Мы видим, что количество томатов и огурцов представлены в виде смешанных чисел:

Чтобы посчитать требуемую массу, нужно выполнить сложение смешанных чисел. Для этого, мы должны отдельно сложить все компоненты. Однако, дробные части, отличаются цифрами под дробной чертой, поэтому используем правило:

Следуя правилу, приведем составляющие смешанных чисел к общему значению, стоящему под числителем. Так как два и три являются взаимно простыми числами, то НОЗ будет равен произведению данных чисел:
НОЗ(2;3) = 2×3 =6.
Соответственно, две третьих необходимо умножить на два, а одну вторую нужно умножить на три.
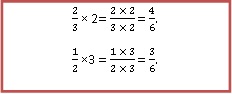
В результате получили дроби с одинаковыми знаменателями.
Найдем сумму значений:


Вначале, найдем НОЗ для трех восьмых и шести седьмых. Разложим цифры, стоящие под чертой на составляющие:

Расклады, не имеют общих составляющих, поэтому числа являются взаимно простыми, значит, их произведение и будет НОЗ:
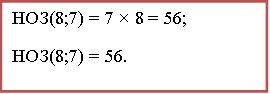
Определим дополнительные множители:
56 : 8 = 7 ;
56 : 7 = 8.
Приведем дроби к общему числовому значению под числителем:
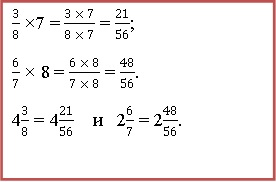
Пока провести операцию, отвечающую на главный вопрос задачи не представляется возможным, ведь составляющая уменьшаемого, представленная в виде дроби, меньше, чем вычитаемого. Используя изученное определение, представим 4*(21/56) в виде дробного числа, в котором значение над чертой будет больше, чем под нею. Для этого представим в виде суммы:


Интересные факты
- Самая большая снежинка, согласно сообщениям ученых в диаметре достигла одной второй (половины) метра, а в толщине одной пятой метра или 20 сантиметров.
- Самый большой слиток золота в мире равен одной четвертой тонны, то есть 250 килограммов.
- 97/100 всей воды в мире, является соленой и не пригодной для использования в пищу,две сотых всей мировой влаги – ледники, её использование так же невозможно. Только одна сотая живительной влаги годится для употребления человеку.
- Наша планета на три четвертых состоит из жидкости, когда космонавты впервые увидели землю из открытого космоса, она показалась им голубым шаром. С тех пор Землю и называют «голубой планетой».
- Согласно заявлениям экологов,человеком, на земле уже уничтожено четыре пятых всех лесных массивов.
- Обычная блоха в прыжке преодолевает расстояние, превышающее её длину в 130 раз. Если бы блоха имела рост 1 м 80 см, то её прыжок составлял бы одну четвертую километра или 250 метров.
ВОПРОСЫ И ЗАДАНИЯ
Чтобы сложить дроби 1/4 и 5/9 нужно:
1) привести дроби к общему знаменателю 2) отдельно сложить числители, а отдельно знаменатели 3) сложить числители, а знаменатели оставить без изменения
Смешанное число – это…:
1) число, состоящее из целой и дробной части 2) число, состоящее из числителя и знаменателя 3) число, состоящее из 3 цифр
Чтобы найти сумму двух смешанных чисел нужно:
1) сложить целые части, а дробные оставить без изменения 2) сложить дробные части, а целые оставить без изменения 3) отдельно сложить целые части и отдельно сложить дробные части
Вычислите разность ½ - ¼:
1) 1/5 2) 1/4 3) 1/8
Выберите верное равенство:
1) 1*3/5 < 2*3/5; 2) 4/5 = 5/9 3) 1*3/5 > 2*3/5



