План урока:

Скорость прямолинейного равноускоренного движения и ее график

Перемещение прямолинейного равноускоренного движения

Относительность механического движения

Различные взгляды на строение Вселенной

Скорость прямолинейного равноускоренного движения и ее график

В математике изучается линейная функция y = kx + b (x – аргумент, k – постоянный коэффициент, b – свободное число, но для отдельной функции тоже постоянное).

Например, пусть в первые дни уборки помидоров было собрано 750 ящиков. А затем бригада растениеводов собирала по 100 ящиков ежедневно. Сколько ящиков помидоров было собрано всего?

Ответ на поставленный вопрос будет зависеть от количества дней работы в поле. Математически это выглядит так: Общее количество набранных ящиков – y, количество дней – x. Значит, у зависит от х. Зависимость одной величины от другой – это уже функция. Постоянный коэффициент k = 100 (одинаковое число ящиков на каждый день уборки). Свободное число b = 750 (число ящиков до того момента, когда начался равномерный прирост количества ящиков). Формула для вычисления примет вид: у = 100х + 750. За последующие 5 дней работники соберут у = 100∙5 + 750 = 1250 (ящиков), за 10 дней – у = 100∙10 + 750 = 1750 (ящиков). Это и есть линейная функция.

Скорость прямолинейного равноускоренного движения, оказывается, является линейной функцией времени. Это подтверждают небольшие преобразования формулы проекции ускорения.

Здесь в качестве примера можно рассмотреть движение автомобиля. Выехав на ровную дорогу, водитель решил увеличить скорость. Пусть в начале он ехал со скоростью 72 км/ч (20 м/с). Затем автомобиль стал передвигаться равноускоренно с постоянным ускорением 2 м/с². Какой станет его скорость через несколько секунд? В этом примере скорость будет зависеть от времени, в течение которого автомобиль разгоняется, то есть скорость – функция времени. Здесь v_ox = 20 м/с, a_x = 2 м/с².

v_x = 2t + 20. За 3 секунды скорость станет v_x = 2∙3 + 20 = 26 (м/с) = 93,6 км/ч, за 4 секунды – v_x = 2∙4 + 20 = 28 м/с = 100,8 км/ч.

Значит, при известных проекциях ускорения и начальной скорости можно всегда найти проекцию мгновенной скорости в конце любого промежутка времени от начала наблюдения. Формула вычисления:

v_ox – начальная скорость. Под этим понятием понимается не скорость в начале какого-либо движения, а скорость в момент времени, когда начинается наблюдение за движением тела.

Простой расчет показывает, что, если тело в начале наблюдения имело скорость v_ox = 0 (находилось в состоянии покоя), то в любой момент времени скорость найдется по формуле:

График линейной функции – это прямая. Пример построения графика зависимости проекции скорости от времени при постоянном ускорении выглядит так:

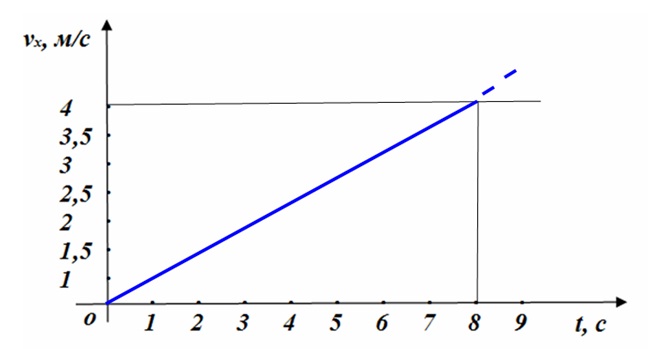
Это график проекции скорости движения, например, лыжника, начинающего спуск с горы из состояния покоя с ускорением 0,5 м/с². Через 8 с его скорость станет 4 м/с. Для построения прямой достаточно знать две точки. В приведенном примере такими точками могут быть координаты начала движения (v_ox = 0, t₀ = 0) и (v_x = 4 м/с, t = 8 c).

Используя график, можно скорость лыжника определить в любой момент времени. Нужно провести перпендикуляры: сначала от оси времени к графику, а затем от графика к оси проекции скорости. Например, через 6 с скорость спортсмена станет 3 м/с.

В случае, если лыжник стал двигаться с горы уже с определенной скоростью v_ox = 2,5 м/с в момент начала наблюдения, прямая линия будет строиться из точки с другими координатами (v_ox = 2,5 м/с, t = 0 c).

На графиках представлено движение лыжника с постоянным ускорением, за счет чего его скорость растет. Векторы скорости и ускорения имеют одинаковое направление.

Теперь другой пример. Пусть санки, скатившись с горы, останавливаются. Если человек, который сидит на санках, специально не предпринимает никаких мер для остановки, санки будут двигаться с постоянным ускорением, направленным против скорости, что уменьшает ее. Такое ускорение создает сила трения, всегда направленная против движения. Это приведет к остановке санок.

В этом случае график проекции скорости выглядит по-другому. Прямая, представляющая график, имеет наклон в другую сторону.

Выезжая с горы на горизонтальную дорожку, санки катились со скоростью 2,5 м/с. Имея примерное значение ускорения 0, 625 м/с², они остановятся через 4 с.

Следует обратить внимание на два существенных момента в графиках:

• Если скорость растет, между графиком и положительным направлением оси t образуется острый угол.

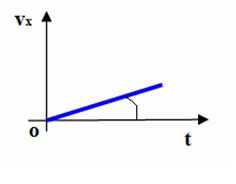
• Если скорость уменьшается, график с положительным направлением оси t образует угол тупой.

Перемещение прямолинейного равноускоренного движения

Перемещение – векторная величина, поэтому вывод формулы перемещения необходимо выполнять, как и для скорости, используя проекции. При прямолинейном равномерном движении проекция перемещения s_x = v_oxt₅ и площадь прямоугольника под графиком скорости S = v_oxt₅ определяются одинаково.

Как же будет выглядеть геометрическая интерпретация равноускоренного движения?

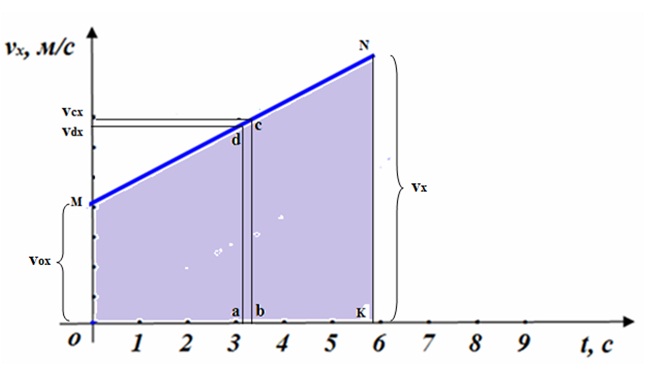
Пусть график скорости представлен отрезком MN, на оси Ot отмечен маленький временной промежуток ab. Проекция скорости меняется от значения v_dx до v_cx.

Рассматриваемое время настолько мало, что скорость в течение его меняется незначительно. Поэтому в такой момент следует считать движение почти равномерным, а геометрическую полосу abcd – почти прямоугольником. Значит, площадь под отрезком dc равна числовому значению проекции перемещения в течение времени ab.

На аналогичные участки разбивается вся фигура OMNK, которая является трапецией.

Площадь трапеции находится умножением полусуммы оснований на высоту. Основания трапеции на чертеже OM (значение начальной скорости v_ox) и KN (значение конечной скорости v_x), высота – ОК (время t).

Значит,

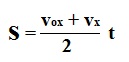
Так как v_x = v_ox + a_xt, и S = s_x, то эту формулу можно привести к новому виду.

И тогда формула для расчета проекции перемещения равноускоренного прямолинейного движения будет следующей:

Пусть тело сначала двигалось со скоростью v_ox = 4 м/с, за 6 секунд его скорость выросла до v_x = 10 м/с. Получается, что за каждую секунду скорость увеличивалась на 1 м/с, то есть ускорение a_x = 1м/с². Тогда пройденный путь s_x = 4∙6 + 1∙6²/2 =24+36/2 = 42 (м).

И по формуле площади трапеции получится s_x = ((4+10)/2)∙6 = 42 (м).

Если тело в начале наблюдения покоилось, то есть v_ox = 0, формула примет более простой вид:

Относительность механического движения

«Механика» - название науки о движении, в переводе с греческого означает «ухищрение, хитрость». Это неудивительно, так как механическое движение, которое называют одним из наиболее простых видов движения, теоретически объясняется довольно непросто.

Примером таких объяснений служат апории (парадоксы) Зенона Элейского (V в. до нашей эры). Самым знаменитым парадоксом Зенона является парадокс «Ахиллес и черепаха», где теоретически доказывается, что быстро бегающий Ахиллес никогда не догонит медлительную черепаху.

Кажется, что это правильно на самом деле.

Пусть в начале движения черепаха находится впереди Ахиллеса на расстоянии a₁. Рассматриваемые объекты начинают движение одновременно. Чтобы догнать черепаху Ахиллес должен сначала за какое-то время преодолеть расстояние a₁. Но черепаха тоже не стоит на месте, она за это время пройдет путь a₂. Ахиллес преодолевает и это расстояние, а черепаха проходит путь a₃. Затем то же самое происходит с расстоянием a₄, и т.д. Так будет до бесконечности. А это значит, что Ахиллес не догонит черепаху никогда.

В действительности, и Ахиллес, и любой человек догонит и перегонит черепаху без труда. В этом и состоит парадокс: теоретически по Зенону черепаху перегнать невозможно, а на практике это сделать легко.

Исторически изучение подобных парадоксов помогало ученым найти истину и дать верное объяснение явлений.

Непростой для понимания законов механического движения является его относительность.

С давних времен систему мира люди называли геоцентрической. Объясняли это тем, что ночные звезды и Солнце днем, в понимании людей, перемещались с востока на запад, а за сутки совершали полный оборот вокруг Земли. Земля считалась центром мира, все космические тела перемещались вокруг нее. Отсюда и название «геоцентрическая система мира».

С развитием науки астрономические исследования стали более точными, появились новые взгляды на строение Вселенной. Система мира была названа гелиоцентрической, так как центром движения планет стали считать Солнце. Планеты по орбитам перемещаются вокруг светила, причем, еще и вращаются вокруг своих осей.

Получается, что в геоцентрической системе движение изучается относительно Земли, а в гелиоцентрической – относительно Солнца.

Развитие научных взглядов на строение Вселенной помогает понять, что одно и то же тело в разных системах отсчета движется по-разному. Это означает относительность движения.

Для более подробного изучения понятия относительности следует рассмотреть по отдельности характеристики движения.

Пусть обычный эскалатор движется со скоростью 0,75 м/с. Нетерпеливый человек, не захотевший просто стоять на нем, идет по ступенькам со скоростью 1 м/с. С какой скоростью передвигается человек? 

Если бы человек стоял на ступеньке, то за одну секунду он переместился бы вместе с этой ступенькой на 0,75 м. Но за эту же секунду он переместился по лестнице на 1 м дополнительно. Значит, за время 1с человек переместился по отношению к стенкам эскалатора не на 0,75 м, а на 0,75 м + 1м = 1,75 м.

Получается, что в системе отсчета, связанной со стенкой эскалатора, скорость пешехода будет 1,75 м/с, а в системе, связанной с лестницей эскалатора – 1 м/с. Как видно из примера скорости различны.

Если бы пешеход по лестнице, двигающейся вниз, пытался подняться вверх, его скорость была бы следующей: 1м/с – 0,75 м/с = 0,25 м/с.

Теперь, как выглядит траектория в разных системах отсчета? Например, всем известно, что колесо велосипеда вертится вокруг оси. Но ведь оно не крутится вокруг дороги, по которой едет велосипедист.

Пусть наблюдение ведется за ниппелем, с помощью которого накачивается колесо велосипеда. По отношению к оси колеса ниппель будет вращаться, и его траекторией является окружность с радиусом, равным по длине спице колеса. А вот по отношению к дороге траектория движения ниппеля будет линией, которая называется циклоидой. Ниппель движется по кривой, периодически то приближаясь к дороге, то отдаляясь от нее.

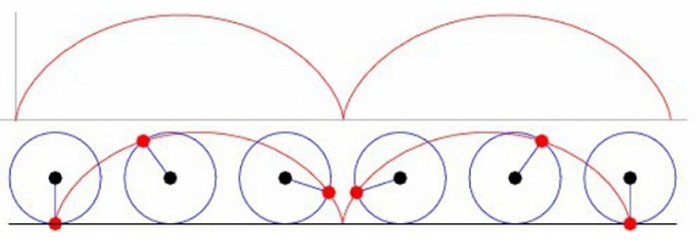
Относительность траектории движения. Источник

Оказывается, траектории тоже различны.

Нетрудно понять, что пройденный путь также относителен. Например, пассажир автобуса по отношению к самому автобусу находится в покое, и пройденный путь его равен 0. Относительно же Земли путь пассажира имеет определенное значение, так как происходит движение по отношению к системе отсчета, связанной с Землей.

Различные взгляды на строение Вселенной

Во II веке, когда в среде древних ученых использовалась геоцентрическая система мира, ученым из Александрии Клавдием Птолемеем были составлены таблицы, по которым определялись положения небесных тел в будущем и прошлом. По этим таблицам рассчитывались наступления солнечных и лунных затмений, возможные траектории движения комет. По тем временам взгляды на строение Вселенной были довольно прогрессивными.

Новый взгляд на движение во Вселенной был изложен польским ученым Николаем Коперником. Это было уже в XVI веке, и учение Коперника подвергалось жесточайшей критике со стороны инквизиции^[1].

Гелиоцентрическая система мира за тело отсчета принимает Солнце. Тогда как объяснить суточное обращение главного светила вокруг Земли, ведь человек находится на Земле и воспринимает это небесное тело связанным с системой отсчета?

Но, например, при плавном начале движения теплохода от пристани пассажирам тоже кажется, что движутся не они вместе с теплоходом, а пристань отплывает назад.

Вращаясь вместе с Землей, человек видит перемещение Солнца, а не перемещение Земли. На самом деле у планеты существует незримая ось вращения, проходящая через Северный и Южный географические полюсы Земли. За двадцать четыре часа Земля совершает полный оборот вокруг этой оси. Данный период времени называется сутками. За сутки человек успевает наблюдать, как то место, где он находится, то освещается Солнцем, то попадает в темноту. Поэтому наблюдателю кажется, что светило то всходит и освещает все вокруг, то заходит, и наступает ночь.

Источник

Значит, видимое обращение Солнца объясняется суточным вращением Земли вокруг своей оси.

Подход к строению Солнечной системы, как к гелиоцентрической, оказал огромное влияние на дальнейшее развитие учений о Вселенной. Это помогло открытию новых физических законов и теорий.

Итак, неотъемлемой чертой механического движения является его относительность:

• без тела отсчета нет смысла говорить о движении;
• одно и то же движение выглядит неодинаково (различные скорости, пройденный путь, траектория) относительно разных тел отсчета (Земли, Солнца, поезда, самолета, дома и т.д.).

Однако наряду с относительностью механическое движение обладает абсолютными свойствами.

Например, если два автомобиля едут навстречу друг другу, то где бы ни находился наблюдатель (на Земле, Луне, на дереве, в одном из автомобилей и т.д.), он будет фиксировать сближение этих автомобилей. Сближение двух объектов в этом примере будет иметь абсолютный характер, то есть для любого тела отсчета движение будет рассматриваться одинаково, как сближение. В отличие, например, от случая: для человека на пристани теплоход отдаляется, пристань стоит, а для пассажира теплохода пристань отдаляется, а теплоход не меняет положения по отношению к пассажиру.

Словарь

1. Инквизиция – созданные в средние века в Западной Европе духовные суды, направленные против атеизма, научных теорий, которые считались ересью.