План урока:

Предмет стереометрии

Основные понятия стереометрии

Аксиомы стереометрии

Простейшие следствия из аксиом стереометрии

Задачи на использование аксиом

Предмет стереометрии

В 7-9 классах мы изучали только те геометрические фигуры, которые полностью лежат в одной плоскости. Грубо говоря, все построения, которые мы делали на уроках, можно было точно выполнить на листе бумаги. Тем самым мы могли проверить с помощью построения, правильно ли решена та или иная задача. На самом деле мы изучали только один раздел геометрии – планиметрию, которая как раз рассматривает построения на плоскости и свойства плоских фигур.

Однако в реальности мир значительно сложнее. Наше пространство считается трехмерным, и большинство реальных объектов обладают объемом. Свойства фигур в пространстве изучает специальный раздел геометрии – стереометрия.

Сразу заметим, что при изучении стереометрии используются все те знания, которые были получены в рамках планиметрии.

Основные понятия стереометрии

Стереометрия оперирует всеми теми понятиями, которые нам известны из планиметрии – точка, прямая, окружность, треугольник и т. д. Но помимо них добавляются и иные термины.

Важнейшее из основных понятий стереометрии – это плоскость. Иногда в литературе применяется сокращение плос-ть. Строгого определения плоскости в рамках геометрии не дают, это понятие считается исходным, как понятия точки или прямой в планиметрии. Лишь некоторые ее свойства косвенно указываются с помощью аксиом. В реальной жизни примерами плоскости являются поверхность стола или лист бумаги. Однако, в отличие от них, плоскость не имеет границы, она бесконечна (как и прямая). Плоскость не имеет кривизны, поэтому, например, поверхность шара плоскостью не является. При изображении плоскости на чертежах ее обычно показывают в виде параллелограмма, при этом традиционно их обозначают маленькими буквами греческого алфавита, которые в планиметрии используются для обозначения углов (α, β, γ и т. п. ):

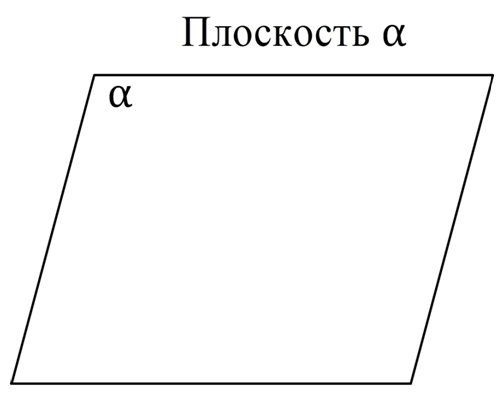
Если на плоскости проведена прямая, то она разобьет ее на две фигуры, которые именуются полуплоскостями:

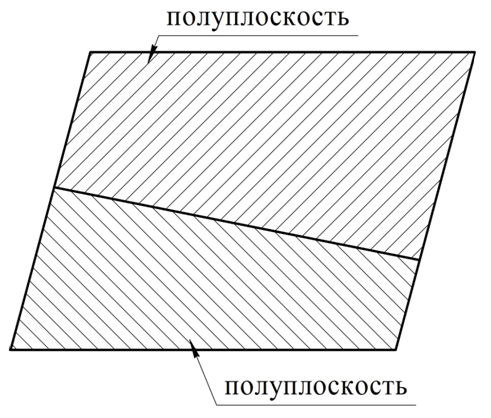
Объемные фигуры – это часть пространства, которая отделена от остального пространства замкнутой поверхностью, то есть границей. Простейший пример объемной фигуры – это куб:

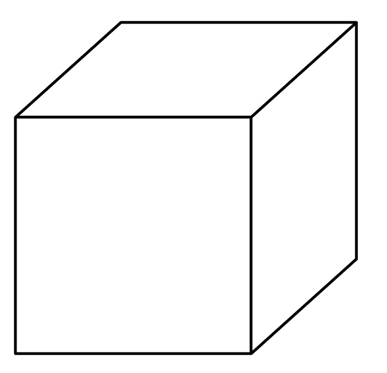
Поверхность куба – это 6 равных квадратов, каждый из них именуется гранью куба. Стороны этих квадратов – это уже ребра куба, а вершины квадратов одновременно являются и вершинами кубов.

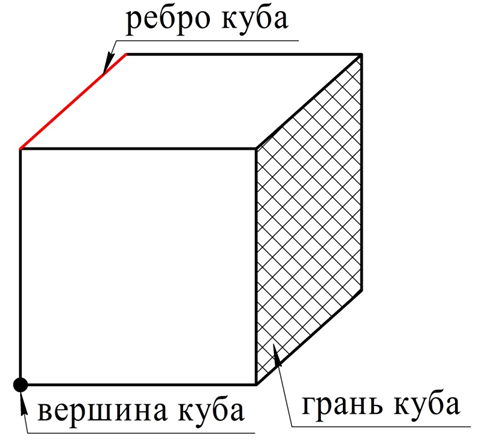
Обратите внимание на изображение куба. Здесь он показан немного сбоку, в результате чего изображение становится объемным. Однако при этом мы вынуждены искажать некоторые размеры и углы на чертеже. Например, верхняя грань должна быть квадратом, но на плоском рисунке углы у этой грани прямыми не являются. При необходимости мы просто ставим специальный значок перпендикулярности между отрезками, который использовали и в планиметрии:

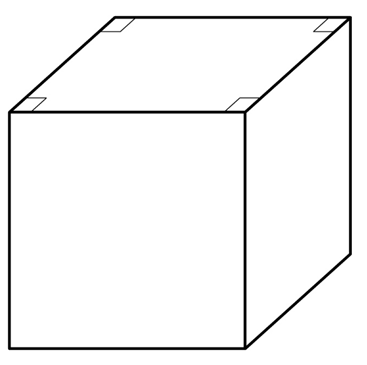
Важно понимать, что из-за искажения размеров у объемных фигур на плоских чертежах мы НЕ можем проверить решение некоторых стереометрических задач с помощью точных построений. Однако есть специальные компьютерные программы 3-D черчения, в которых такие построения уже можно выполнить. Также заметим, что на рисунке видны не все 6 граней куба, а только 3 из них. Если возникает необходимость показать невидимые на чертеже линии, то использует штриховые линии:

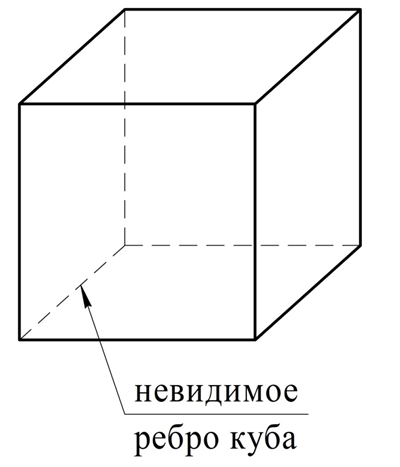
Все грани куба – это многоугольники. Если у фигуры вся ее поверхность состоит лишь из многоугольников, то она именуется многогранником. Таким образом, куб является примером многогранника. Другими примерами многогранников могут служить параллелепипед, пирамида, усеченная пирамида:

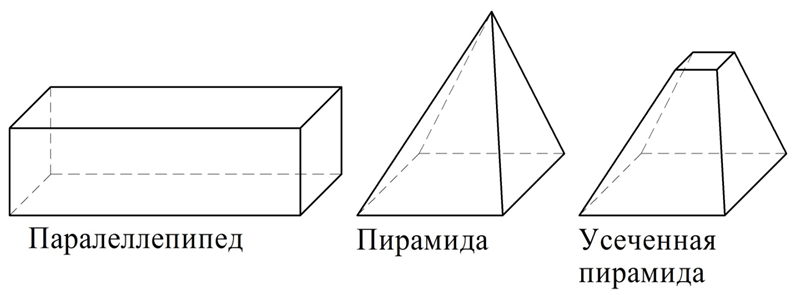
Более подробно различные виды многогранников будут рассматриваться позднее, тогда же им будут даны и их определения.

Если у объемной фигуры хоть одна поверхность не является многоугольником, то она не может считаться многогранником. Наиболее простыми и часто встречающимися такими фигурами являются шар, цилиндр, конус. Обратите внимание, что у них могут отсутствовать ребра и вершины, которые обязательно есть у многогранника:

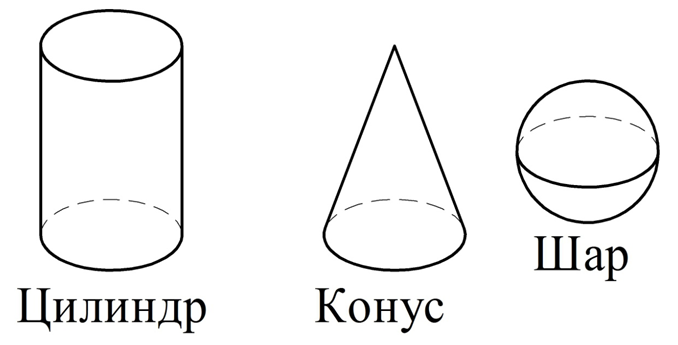
Следует различать саму объемную фигуру и ее границу. Так, шар – это объемная фигура, а поверхность шара – это сфера.

Аксиомы стереометрии

Стереометрия, как и планиметрия, построена на нескольких базовых утверждениях, которые считаются абсолютно очевидными и не требуют доказательств. Их называют аксиомами. В свою очередь на основе аксиом доказываются простейшие теоремы стереометрии, которые далее используются для доказательства других, более сложных теорем и т. д. Грубо говоря, аксиомы – это исходные, первичные теоремы, принимаемые без доказательств.

Все вместе аксиомы образуют так называемую систему аксиом, или аксиоматику. Система аксиом должна быть непротиворечивой, то есть с ее помощью нельзя одновременно доказать и истинность, и ложность одной и той же теоремы. Также она должна быть ещё и независимой. Это значит, что ни одна из аксиом не может быть доказана с помощью других аксиом (в противном случае эту аксиому можно просто исключить из списка аксиом и считать ее теоремой). Наконец, аксиоматика должна быть полной, то есть с ее помощью любую теорему можно либо доказать, либо опровергнуть, а недоказуемых теорем быть не должно.

На самом деле вопрос о выборе системе аксиом в любой математической дисциплине, в том числе и в геометрии, является достаточно сложным. Первую аксиоматику сформулировал ещё Евклид, но в дальнейшем она была признана не вполне удачной. На сегодняшний день наибольшее распространение получила система аксиом Гильберта, которая была сформулирована только в 1899 г. Однако помимо неё существует ещё несколько аксиоматик: Погорелова, Колмогорова, Вейля, Биргофа и. т. д.

Прежде, чем формулировать сами аксиомы, ещё раз уточним, что есть так называемые неопределяемые понятия стереометрии. В аксиоматике Гильберта это плоскость, точка и прямая. Их свойства как раз и описываются аксиомами. Остальным понятиям даются определения, многие из них были сформулированы в 7-9 классах.

Всего в аксиоматике Гильберта есть 20 аксиом. Из них 15 относятся к планиметрии, и только 5 – к стереометрии. Сначала сформулируем две аксиомы о трех точках:

Здесь приведены два различных утверждения, поэтому их принято разделять на две отличных аксиомы. Для простоты запоминания их можно объединить в одно утверждение:

Другими словами, любые три точки находятся в одной плоскости. По этой причине для обозначения плос-тей иногда просто указывают три ее точки (важно, что они не должны принадлежать одной прямой).

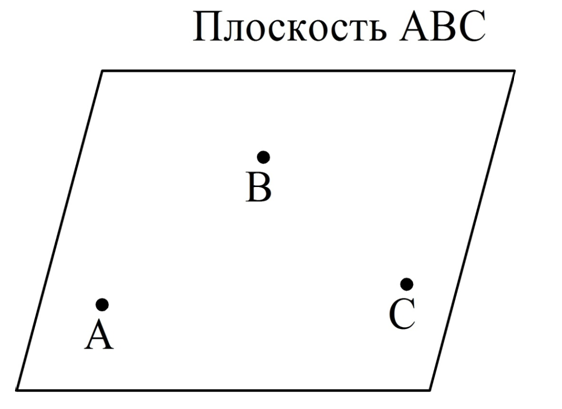
Иногда используются утверждения, что три точки однозначно задают плос-ть или однозначно ее определяют.

Случай, когда три точки находятся на одной прямой, рассматривается отдельно и чуть ниже.

Далее сформулируем аксиому о четырех точках:

Сформулированные три аксиомы стереометрии легко подтверждаются примером из жизни. Возьмем стул с тремя ножками. Мы можем твердо установить его на пол, даже если длина ножек не одинакова. Однако, если у стула 4 ножки, то иногда (когда ножки стула имеют разную длину), стул начинает «шататься». Тремя точками он будет касаться пола, а четвертая опора будет висеть в воздухе. Это происходит из-за того, что 4 конца ножек могут находиться в разных плоскостях. У стула с тремя ножками такая ситуация невозможна, так как его концы ножек в любом случае окажутся в одной плос-ти.

Следующая аксиома отражает связь плос-ти и прямой:

Эту аксиому также подтверждает жизненный опыт. Если отметить на ровном столе любые две точки и приложить к ним ровную линейку, то контакт между линейкой и столом будет плотным, то есть без зазоров. Если же какие-то зазоры есть, то это свидетельствует лишь о неровности стола либо линейки.

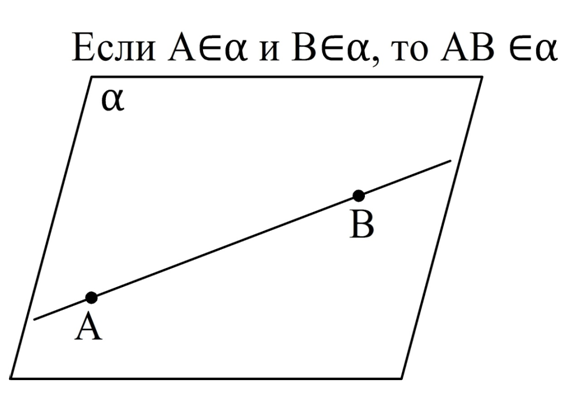
Напомним, что в математике есть специальный символ «∈», который показывает, что один объект является частью другого, то есть, принадлежит ему. Так, если прямая АВ лежит в плос-ти α, то этот факт можно показать записью АВ∈α.

Возможен случай, когда прямая имеет с плос-тью единственную общую точку. В таких случаях принято говорить, что прямая и плос-ть пересекаются:

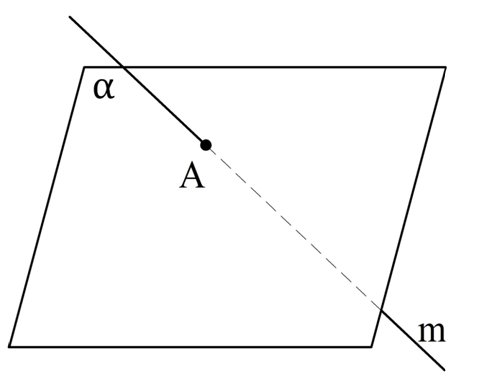
Последняя, пятая аксиома говорит о пересечении двух плос-тей.

Действительно, сложно представить себе ситуацию, когда две плос-ти коснулись друг друга только в одной точке. На основе сформулированных аксиом легко доказать одно из простейших и вместе с тем важнейших утверждений стереометрии.

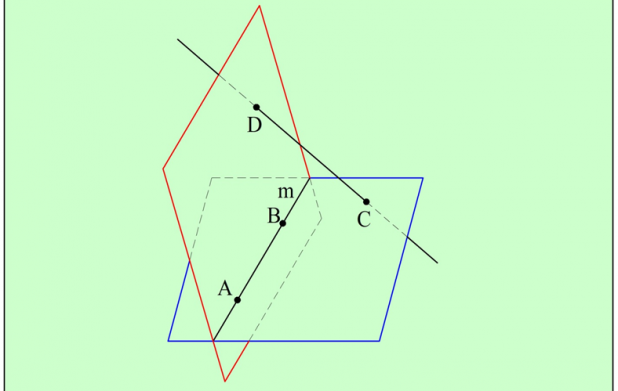
Действительно, пусть у двух плос-тей, α и β, есть общая точка А. Тогда, согласно аксиоме 5, у них должна быть и другая общая точка, которую мы обозначим как В:

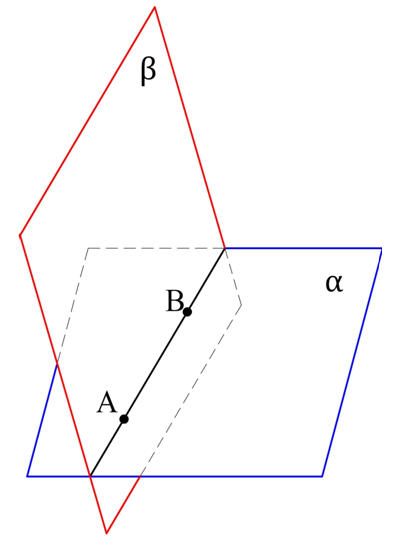
Рассмотрим прямую АВ. По аксиоме 4 она полностью принадлежит плос-ти α, ведь α принадлежат две ее точки. По той же причине можно утверждать, что АВ также принадлежит и β. Таким образом, АВ – общая прямая для α и β.

Но нам надо также показать, что никакая другая точка в пространстве не является общей для α и β. Действительно, пусть существует ещё и некоторая точка С, которая НЕ лежит на АВ, но является общей для α и β. Это означало бы, что через А, В и С проведены две различные плос-ти (α и β). Это противоречит аксиоме 2, поэтому такая точка С не существует, ч. т. д.

Вернемся к аксиомам 1 и 2. В них говорилось о 3 точках, причем отдельно оговаривалось, что они не должны принадлежать одной прямой. Теперь нам ясна причина этой оговорки. Только что доказанная теорема показывает, что через прямую (а значит, и через любые 3 ее точки) может проходить не одна, а как минимум 2 плос-ти. В дальнейшем мы покажем, что на самом деле через прямую можно провести бесконечное число плос-тей.

Простейшие следствия из аксиом стереометрии

На основе аксиом можно доказать несколько простых теорем стереометрии.

Доказательство. Возьмем произвольную прямую m и точку C, которая НЕ принадлежит m. Далее отметим на m две любые точки и обозначим их как А и В:

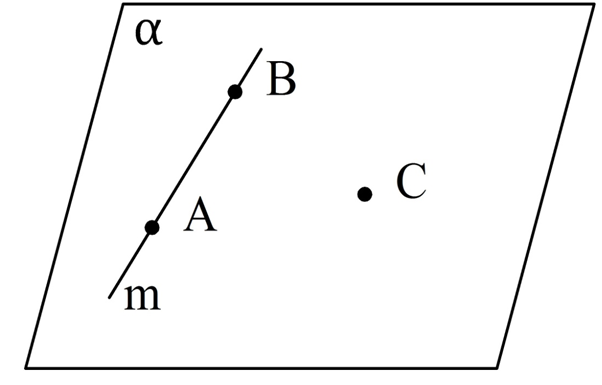
По аксиоме 1 через А, В, С можно провести некоторую плос-ть α. По аксиоме 4 прямая m будет принадлежать α. Тем самым мы показали, что существует плос-ть, проходящая через m и C. Единственность этой плос-ти вытекает уже из аксиомы 2, ведь через А, В и С нельзя провести две различных плос-ти, ч. т. д.

Иногда доказанный факт формулируют иначе: прямая и точка, не находящаяся на прямой, однозначно определяют проходящую через них плос-ть. То есть, указав прямую и точку, можно одновременно указать на ту плос-ть, которая задается ими.

Переходим к следующей теореме.

Отметим на произвольной прямой m точки А и В. Далее выберем ещё две точки в пространстве C и D, причем такие, что А, В, С и D не находятся в одной плос-ти. Тогда у нас есть плос-ти АВС и АВD, которые пересекаются по прямой АВ:

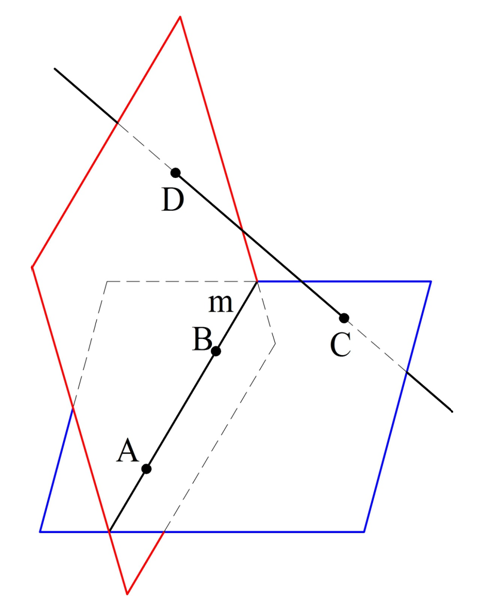
Теперь соединим С и D прямой. Прямая CD состоит из бесконечного количества точек. Через каждую из них можно провести единственную плос-ть, которая будет проходить через АВ. Так как точек бесконечно много, то и плос-тей будет бесконечно много. Осталось лишь показать, что никакие две таких плос-ти не будут совпадать, то есть все они различны.

Действительно, пусть две таких плос-ти совпадают, то есть на самом деле являются одной плос-тью. Тогда получается, что эта единая плоскость проходит через две точки прямой СD. Тогда, по аксиоме 4, вся прямая СD принадлежит этой плос-ти, в том числе и сами точки С и D. Но плос-ть проходит также через А и В. То есть получится, что А, В, С и D входят в состав одной плос-ти, а это не так. Это противоречие означает, что на самом деле все плоскости, проходящие через разные точки прямой CD, будут различны, ч. т. д.

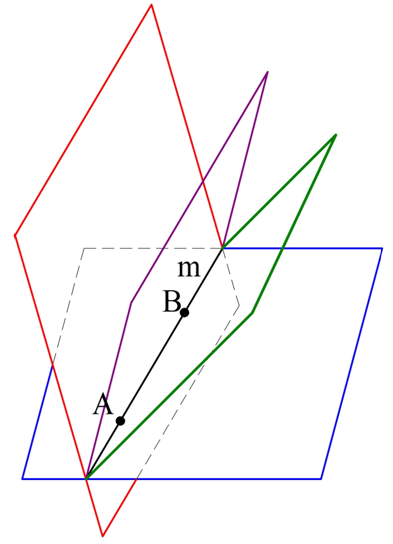
Рассмотрим ещё одну теорему:

Пусть пересекаются прямые m и n. Обозначим точку их пересечения как А. Также выберем на m некоторую точку В, а на n – точку C. Мы можем построить плос-ть α через точки А, В и C, и она будет единственной. Так как и А, и В принадлежат α, то и вся прямая m ей принадлежит (аксиома 4). Аналогично и прямая n находится на плос-ти α. То есть α как раз и является плос-тью, о которой говорится в теореме. Никакая другая плос-ть не будет содержать обе прямые m и n, ведь в противном случае она проходила бы через точки А, В и С, то есть совпадала бы с α.

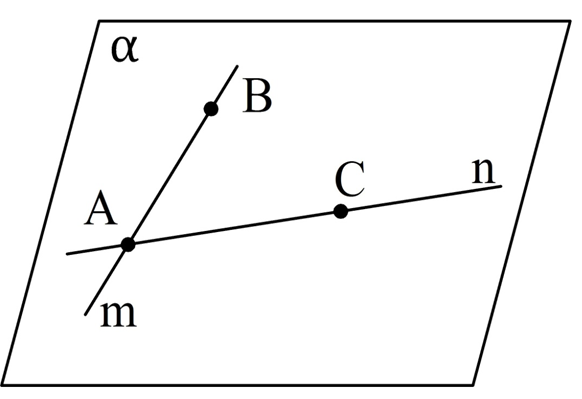
Эта теорема также говорит о том, что две пересекающиеся прямые однозначно определяют проходящую через них плос-ть.

Задачи на использование аксиом

Простейшие задачи стереометрии по большей части не требуют проведения расчетов и использования формул, однако приходится использовать строгие логические умозаключения. Чаще всего они сводятся к доказательству довольно очевидных утверждений.

Примечание. Попытайтесь перед просмотром решения задач самостоятельно их решить.

Задание. Точки M, N, Р, К не лежат на одной прямой. Могут ли прямые MN и РК пересекаться?

Решение. Если бы MN и РК пересекались бы, то через эти прямые можно было бы провести плос-ть. Эта плоскость содержала бы все точки прямых, в том числе M, N, Р и К. Но эти точки по условию не могут принадлежать одной прямой. Значит, MN и РК не пересекаются.

Задание. Есть 4 точки, из которых три принадлежат одной прямой. Могут ли эти точки не лежать на единой плоскости?

Решение. Пусть точки Р, К, М находятся на единой прямой РК, а Н – ещё одна точка. Если Н также лежит на РК, то мы можем построить бесконечно много плос-тей, проходящих через РК, и каждая из них будет содержать все эти четыре точки. Если же Н не принадлежит РК, то всё равно через РК и Н можно провести плос-ть, но на этот раз единственную. И эта плос-ть также будет содержать в точки Р, К, М и Н. В любом случае получается, что эти точки находятся на одной плос-ти.

Задание. Через пересекающиеся прямые m и n проведена плоскость α. Верно ли, что любая прямая h, пересекающая m и n в различных точках, будет также принадлежать α?

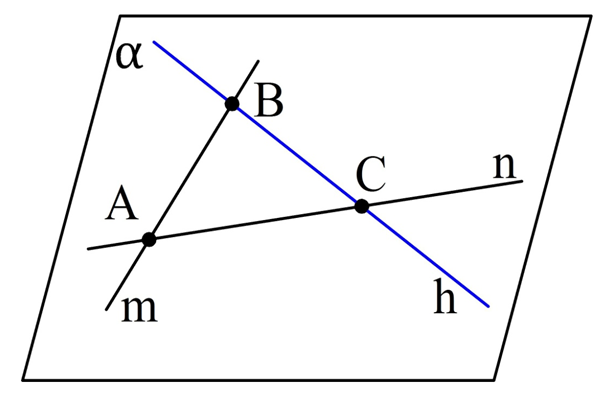
Решение. Пусть прямая h пересекает m и n в точках В и C соответственно. Раз эти точки принадлежат прямым m и n, то они принадлежат и плос-ти α. Получается, что две точки прямой h (В и С) находятся на α. Тогда, по аксиоме 4, и вся прямая h также находится на α. То есть утверждение, сформулированное в условии задачи, верно.

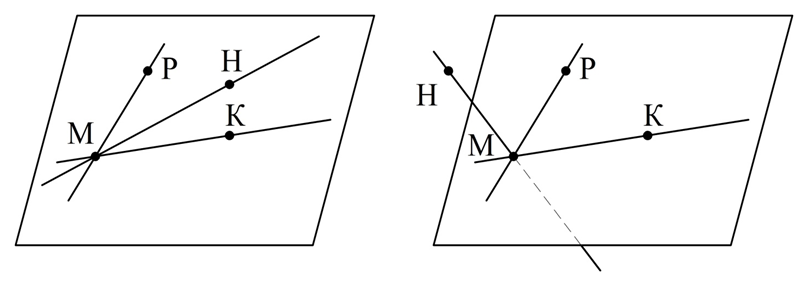
Задание. Три прямые проходят через общую точку M. Верно ли, что они находятся в одной плоскости?

Решение. Неверно, они могут как находиться, так и не находиться в одной плоскости. Оба случая проиллюстрируем примерами. Пусть есть точки М, Р, К и Н, причем они одной плос-ти не принадлежат. Тогда прямые МР, МК, МН пересекаются в М, но находятся в одной плос-ти. Если же мы выберем точки М, Р, К, Н так, чтобы они находились на единой плос-ти, то прямые МР, МК, МН пересекутся в М и будут принадлежать одной плос-ти.

Задание. Плос-ти α и β не пересекаются. Прямая m пересекает α. Докажите, что она также пересекает и β.

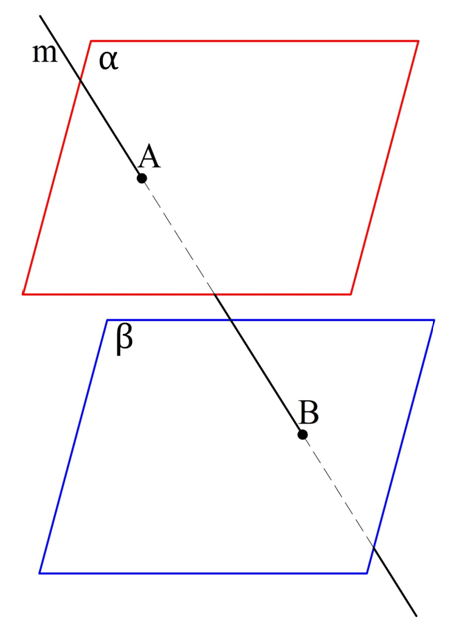
Решение. Сразу скажем, что эта задача сложнее предыдущих, и ее решение неочевидно. Дадим подсказку: при решении стереометрических задач можно использовать и аксиомы планиметрии, в том числе и знаменитую аксиому о параллельных прямых.

Теперь приведем решение. Пусть m пересекает α в точке А. Отметим на β произвольную точку С. Теперь мы можем провести ещё одну плос-ть γ через прямую m и точку C:

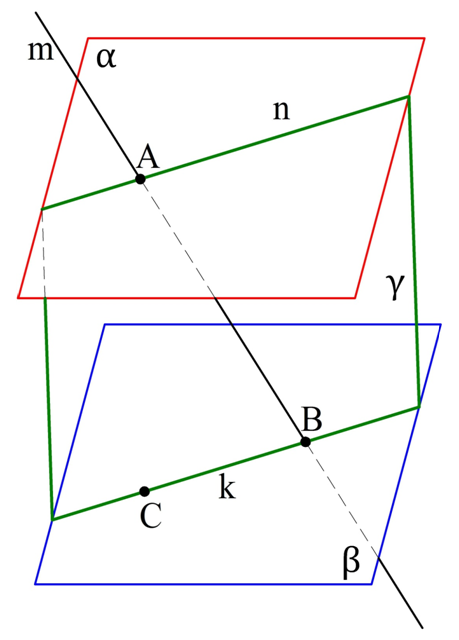
Плос-ти γ и β имеют общую точку С. Значит, они пересекаются по некоторой прямой k. У плос-тей γ и α есть общая точка А, поэтому и они пересекаются по некоторой прямой n.

Теперь проанализируем расположение прямых n и k. Они не могут пересекаться, ведь тогда бы точка их пересечения была общей для α и β, а они не пересекаются. Также n и k лежат в одной плос-ти. Тогда n и k по определению параллельны.

Напомним, что по аксиоме параллельности через точку на плос-ти может быть проведена лишь одна прямая, параллельная заданной прямой. В частности, через точку А мы можем провести только одну прямую, параллельную k. Такая прямая уже проведена – это n. Тогда вторая прямая, проходящая через А (это как раз m) либо совпадает с n, либо пересекает k. Совпадать с n она не может, ведь в этом случае m будет полностью принадлежать плос-ти α, а она по условию лишь пересекает ее. Значит, m должна пересечь k в некоторой точке В. Эта точка В принадлежит прямой k, а значит, находится и на плос-ти β. Тем самым мы показали, что m и β пересекаются в точке В.

Для полноты доказательства надо ещё показать, что m имеет ровно одну общую точку с В. Действительно, если бы была ещё одна общая точка, то по аксиоме 4 вся прямая m находилась бы на β. Тогда и точка А оказалась бы на β, то есть она стала бы общей точкой α и β, но таких общих точек по условию не существует, ч. т. д.

Задание. Четыре точки в пространстве выбраны так, что никакая прямая, проходящая через две из этих точек не пересекается с прямой, проходящей через другие две точки. Могут ли эти четыре точки находиться на одной плос-ти?

Решение. Предположим, что есть точки М, Р, К и Н, удовлетворяющие условию задачи и находящиеся на одной плос-ти. Ясно, что никакие три из этих точек не принадлежат одной прямой. Тогда мы можем построить четырехугольник МРКН.

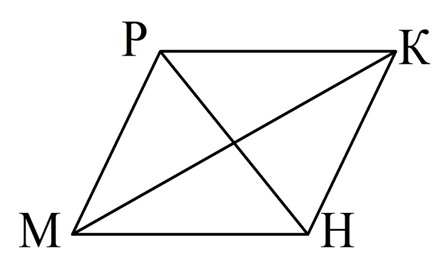
Прямые МР и КН по условию не должны пересекаться, то есть они параллельны. Аналогично параллельны МН и РК. Значит, МРКН – параллелограмм по его определению. Но в параллелограмме пересекаются диагонали МК и РН, а по условию и эти прямые не должны пересекаться. Получили противоречие. Из него вытекает, что М, Р, К и Н НЕ могут находиться на одной плоскости.

В ходе сегодняшнего урока мы познакомились с понятием стереометрии. Именно этот раздел геометрии мы будем изучать в течение 10 и 11 класса. Мы узнали о пяти основных стереометрических аксиомах следствиях из них. Использование аксиом в учебном процессе не только позволяет понять геометрию, но и развивает навыки строгого логического мышления, так необходимые в современном мире.