Геометрия
Скрещивающиеся прямые
План урока:
Задачи на скрещивающиеся прямые
Понятие скрещивающихся прямых
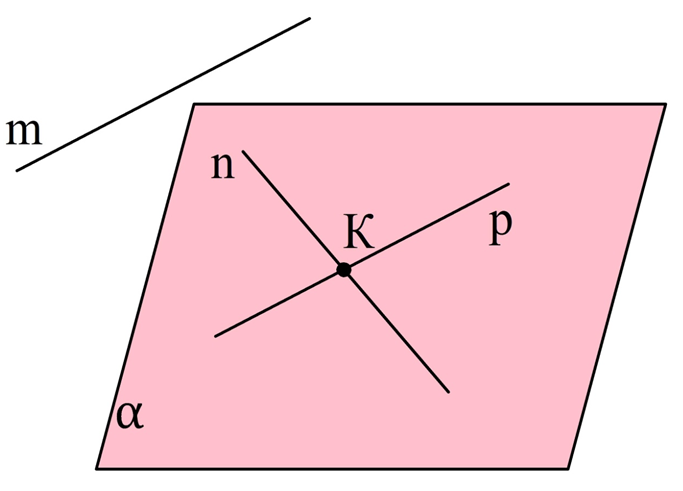
В пространстве можно построить две прямые так, что они не будут пересекаться, но и параллельными они также являться не будут. Для этого достаточно, чтобы прямые НЕ находились в одной плоскости. В этом случае их именуют скрещивающимися прямыми.
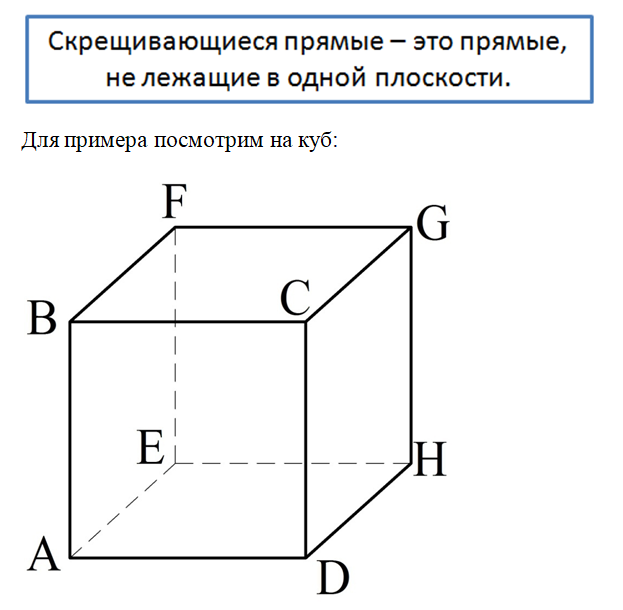
Здесь ребра ВС и АЕ как раз лежат на двух скрещивающихся прямых. Поэтому их можно так и называют – скрещивающиеся отрезки. По аналогии можно ввести понятие и скрещивающихся лучей.
Существует теорема, представляющая собой признак скрещивающихся прямых.

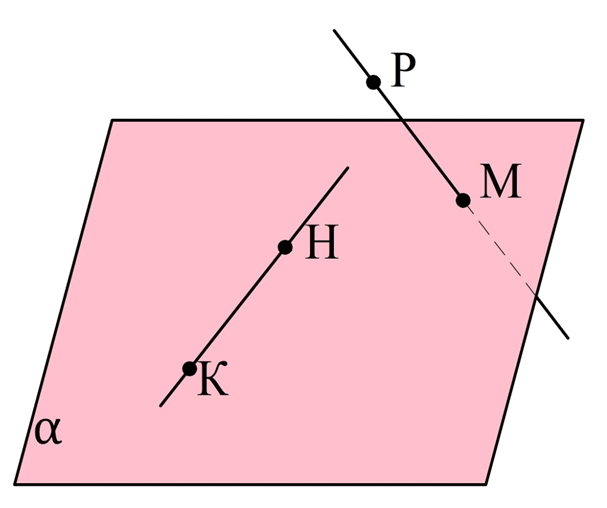
Действительно, пусть есть две прямые, НК и РМ. Обозначим как α плос-ть, проходящую через НК и точку М. Если РМ пересекает α, то это означает, что М – единственная общая точка у α и РМ. Получается, что Н, К, М и Р – это точки в различных плос-тях, и через них нельзя провести одну плос-ть. Значит, и прямые НК и РМ – скрещивающиеся.
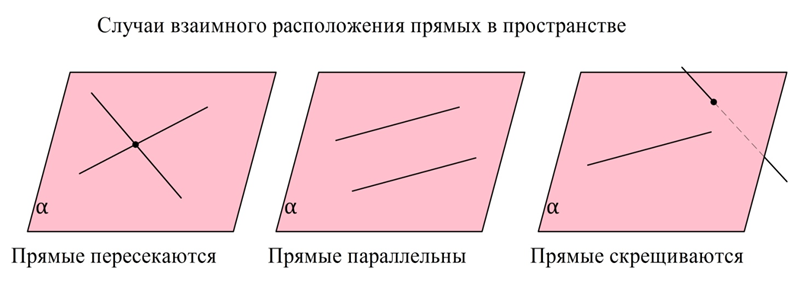
Таким образом, в стереометрии возможно всего три случая взаимного расположения двух прямых в пространстве:
1) прямые пересекаются, и тогда они обязательно находятся в одной плос-ти;
2) прямые располагаются в одной плос-ти, но не пересекаются – случай параллельных прямых;
3) прямые находятся в разных плос-тях – случай скрещивающихся прямых.
Докажем одну теорему:

Для доказательства возьмем произвольные скрещивающиеся прямые m и n. Отметим на n точку К и проведем через К прямую р, параллельную m:
Через пересекающиеся прямые nи p можно провести единственную плос-тьα. По признаку параллельности прямой и плос-ти можно заключить, что m||α.
Покажем, что кроме α нет других плос-тей, проходящих через n и параллельных m. Действительно, если бы такая плос-ть β существовала, то р имела бы с ней общую точку К, но полностью в β она бы не могла находиться, иначе α и β совпадали бы. Значит, р пересекала бы β. Но тогда ее обязательно пересекала бы и m по одну из свойств параллельных прямых. В этом случае m и β не были бы параллельными.
Сонаправленные лучи
В планиметрии существует понятие сонаправленных лучей. Пусть на плос-ти есть два луча О1А и О2В. Проведем прямую О1О2. Она, как и всякая прямая, разделит плос-ть на две полуплоскости. Для того, чтобы лучи О1А и О2В считались сонаправленными, необходимо выполнение двух условий:
1) они должны оказаться в одной полуплоскости;
2) они должны быть параллельными.
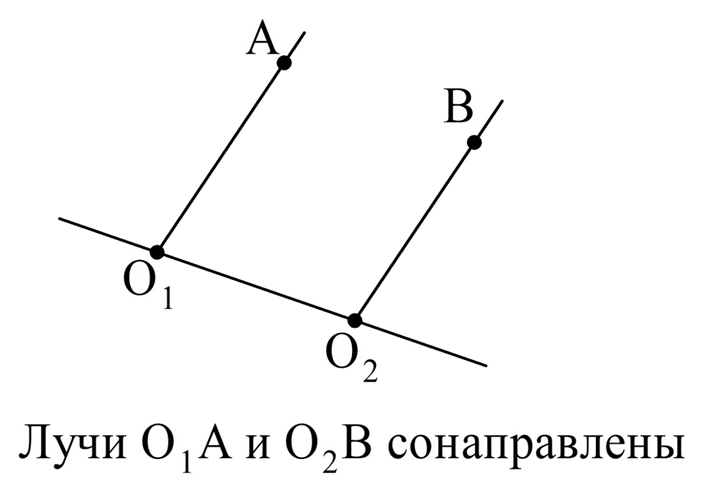
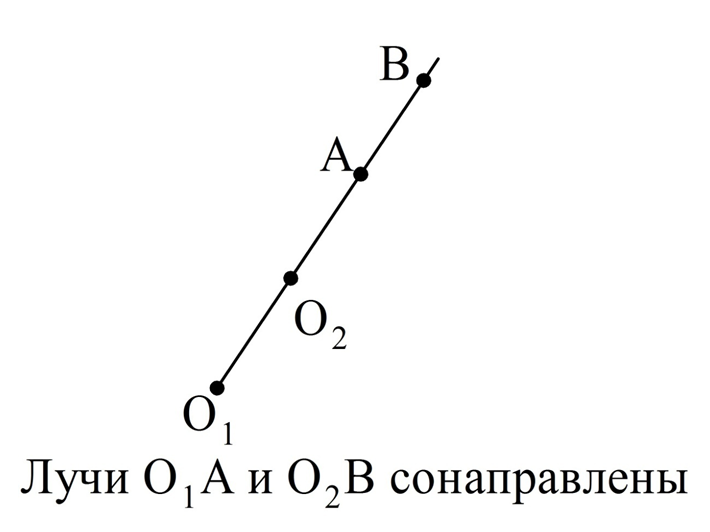
Здесь мы рассмотрели случай, когда лучи О1А и О2В находятся на разных прямых. Возможен частный случай, когда они располагаются на одной прямой. В таком случае для сонаправленности лучей достаточно, чтобы один из них полностью лежал на другом:
Рассмотрим теорему, касающуюся сонаправленных лучей, причем она верна не только в планиметрии, но и в стереометрии.

В доказательстве сразу рассмотрим случай углов, располагающихся в разных плос-тях. Пусть есть углы О1 и О2, стороны которых образуют попарно сонаправленные лучи. На одной паре лучей отметим точки А1 и А2 так, чтобы отрезки О1А1 и О2А2 были одинаковыми. На другой паре лучей аналогично отложим точки В1 и В2 так, чтобы одинаковыми были отрезки О1В1 и О2В2:
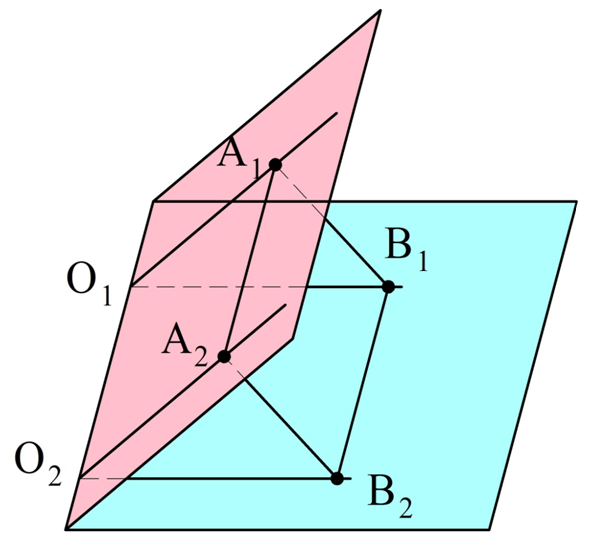
Заметим, что лучи О1А1 и О2А2 как сонаправленные должны располагаться в одной плос-ти, иначе они не будут параллельными. Тогда О1А1А2О2 – плоский четырехугольник. Отрезки О1А1 и О2А2 параллельны и одинаковы. Это значит, что О1А1А2О2 – параллелограмм. Аналогично легко убедиться, что параллелограммом является и четырехугольник О1В1В2О2. Это значит, что
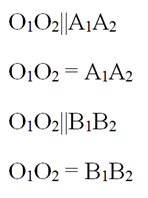
Отсюда вытекает (по свойству транзитивности), что отрезки А1А2 и В1В2 также одинаковы и параллельны, а потому А1А2В2В1 – также параллелограмм. Значит, стороны А1В1 и А2В2 одинаковы. Получается, что у ∆О1А1В1 и ∆О2А2В2 одинаковы все стороны, поэтому ∆О1А1В1 и ∆О2А2В2 равны. Отсюда вытекает и равенство углов ∠А1О1В1 и ∠А2О2В2, ч. т. д.
Угол между прямыми
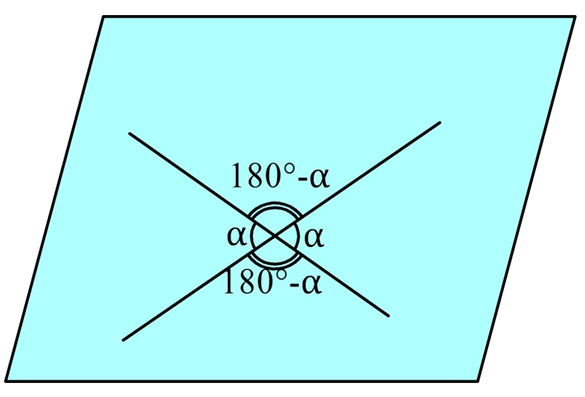
Напомним, какая величина считается углом между пересекающимися прямыми. При пересечении прямых образуется 4 угла. Зная один из них, легко вычислить и остальные углы. Понятно, что хотя бы один из углов будет не превышать 90°. Именно такой угол и принимается за угол между прямыми:
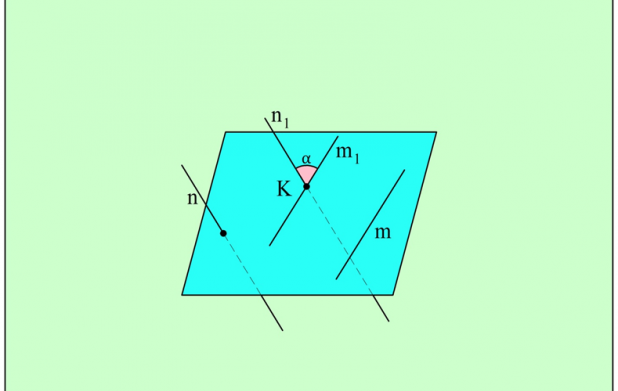
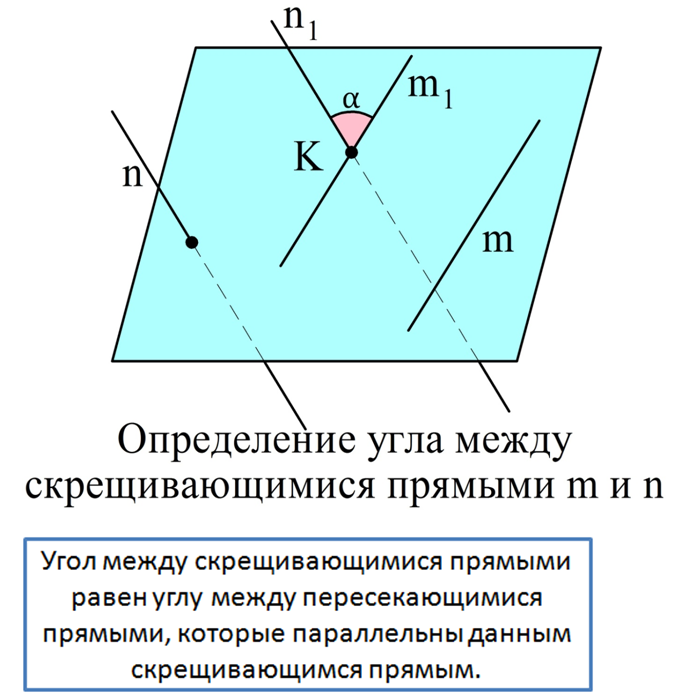
Теперь покажем, как определить угол между скрещивающимися прямыми. Пусть прямые m и n скрещиваются. Выберем в пространстве произвольную точку К. Через нее можно построить такие прямые m1 и n1, что m1||m и n1||n. Угол между m1 и n1 как раз и принимается за угол между скрещивающимися прямыми m и n:
Возникает вопрос – зависит ли величина измеренного таким образом угла от того, какая именно точка К выбрана? Оказывается, что не зависит, и это можно доказать. Выберем две произвольные точки К1 и К2. Через К1 проведем прямые n1 и m1, а через К2 проведем n2 и m2, которые будут соответственно параллельны исходным прямым m и n.
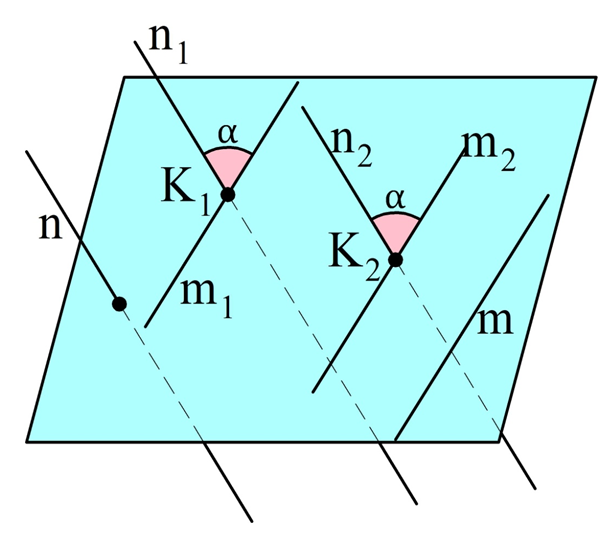
Так как n1||n и n2||n, то по свойству транзитивности параллельности и n1||n2. Аналогично и m1||m2. Получается, что стороны углов в точках К1 и К2 соответственно сонаправлены. Значит, они одинаковы, ч. т. д.
Задачи на скрещивающиеся прямые
Теоретический материал закончился, осталось научиться применять полученные знания. Перед просмотром решения постарайтесь самостоятельно решить каждую задачу.
Задание. Точка D находится вне плос-ти ∆АВС. Середины отрезков АD, BD и СD обозначены буквами M, N и P соответственно. Точка K располагается на отрезке BN (и не совпадает с концами этого отрезка). Определите, как относительно друг друга располагаются прямые:
Решение. Сначала важно построить правильный рисунок по описанию задачи:
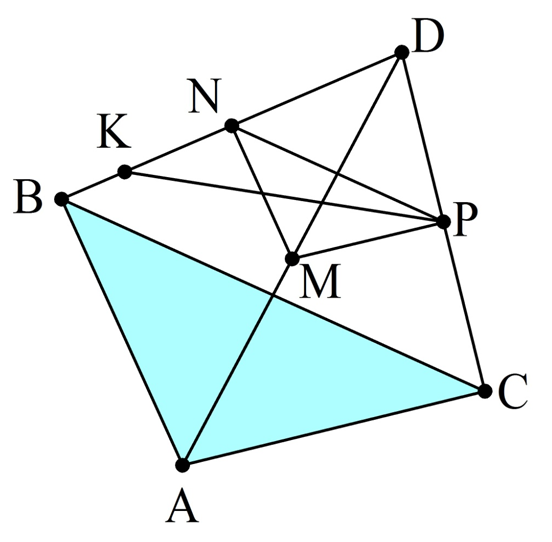
Теперь можно рассмотреть по отдельности каждый пункт.
а) АВ и DN. Прямая DN совпадает с прямой BD. Она в свою очередь пересекается с АВ в точке В. Значит, в данном случае прямые пересекаются.
б) РК и ВС. Рассмотрим плос-ть треугольника ∆ВСD. Рассматриваемые прямые как раз находятся в ней. То есть они уже точно не скрещиваются. Могут ли они быть параллельны? Обратите внимание на отрезок NP. Это средняя линия в ∆ВСD, поэтому NP||ВС. Через Р может быть проведена лишь одна прямая, параллельная ВС (по аксиоме параллельности), и это NP. Значит, KP пересекает ВС.
в) MN и АВ. В ∆АВDMN является средней линией, поэтому MN||АВ.
г) МР и АС. МР – это средняя линия в ∆АСD, значит, МР||АС.
д) KN и АС. Прямая KN совпадает с прямой BD. Она пересекает плос-ть АСВ, но точка пересечения (это В) не находится на АС. Тогда по признаку скрещивающихся прямых можно утверждать, что KN и АС скрещиваются.
е) MD и ВС. MD пересекается с плос-тью АСВ в точке А. Тогда из признака скрещивающихся прямых вытекает, что MD и DC скрещиваются.
Задание. Через точку Р, не находящуюся на прямой m, проведены две различные прямые, не пересекающиеся с m. Верно ли, что хотя бы одна из них точно скрещивается с m?
Решение. Каждая из этих двух прямых с m не пересекается. Тогда они либо параллельны m, либо скрещиваются с ней. Но обе прямые параллельны m не могут быть параллельны m, ведь тогда через Р будет проведено сразу две прямые, параллельные m, что невозможно. Значит, хотя бы одна из прямых действительно скрещивается с m.
Задание. MК и РН – скрещивающиеся прямые.Скрещиваются ли прямые МН и КР?
Решение. Ясно, что точки М, К, Р, Н располагаются в различных плос-тях. В противном случае, если бы существовала плос-ть α, в которой находились бы М, К, Р и Н, то в α также находились бы прямые МК и РН, и тогда они уже по определению не были бы скрещивающимися.
Теперь рассмотрим плос-ть КРН. В ней находится прямая КР. А прямая МН ее пересекает в точке К. Тогда, по признаку скрещивающихся прямых, МН и КР скрещиваются.
Задание. Прямые m и n скрещиваются. M – точка на m, N – точка на n. Через m и N проведена плос-ть α, а через n и M – плос-ть β. Пересекаются ли плос-ти α и β, и если да, то по какой линии?
Решение.
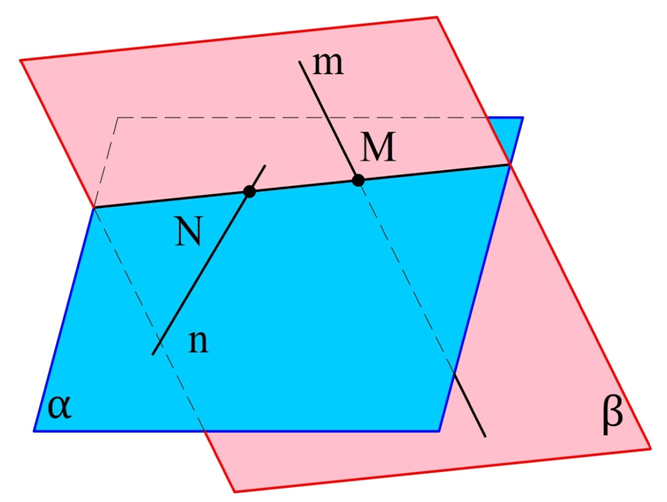
Посмотрим, есть ли у α и β общие точки. Плос-ть α проходит через n, то есть и через точку N тоже. Плос-ть β также проходит через N. Значит, N – общая точка. Аналогично можно показать, что и М – это общая точка. В итоге α и β пересекаются, причем на линии пересечения находятся точки M и N. Значит, именно прямая МN является границей этих двух плос-тей.
Задание. Известно, что MНКЕ – параллелограмм, а МНРТ – трапеция (РТ – её основание), причем они располагаются в разных областях. Каково расположение отрезков КЕ и РТ друг относительно друга.
Решение. Задачу можно решить и без рисунка. Если РТ – основание трапеции, то второе основание – это МН, и МН||РТ. В параллелограмме МНКЕ параллельны стороны МН и КЕ, ведь они противоположные. Тогда по свойству транзитивности параллельности из того факта, что МН||РТ и МН||КЕ, вытекает, что и РТ||КЕ.
Задание. Известно, что ОА и СD – скрещивающиеся прямые, а ОВ||CD. Чему равен угол между ОА и CD, если
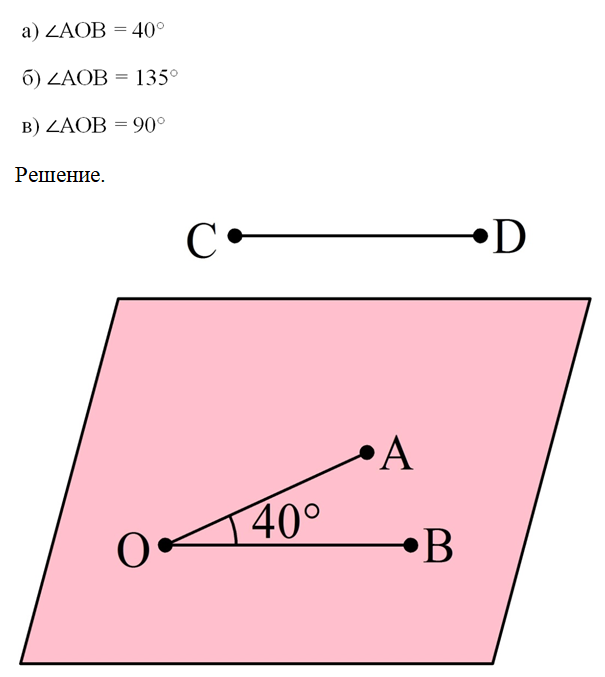
Если CD||ОВ, то угол между CD и ОА совпадает с углом между ОВ и ОА. В задании а) он совпадет с ∠АОВ и составляет 40°. В случае б) угол не может составлять 135°, так как он не должен превышать 90°. Поэтому он равен
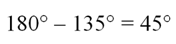
Наконец, в случае в) он составит 90°.
Ответ: а) 40°; б) 45°; в) 90°.
Задание. Дан куб, вершины которого обозначены так, как это показано на рисунке:
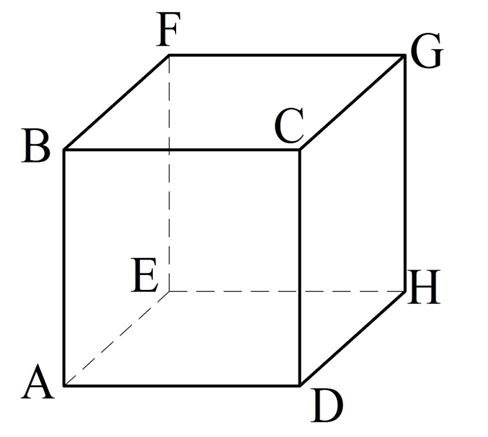
Найдите угол между прямыми:

Решение. Во всех трех случаях нам даны скрещивающиеся прямые. Для вычисления угла надо найти такие параллельные им прямые, которые будут пересекаться.
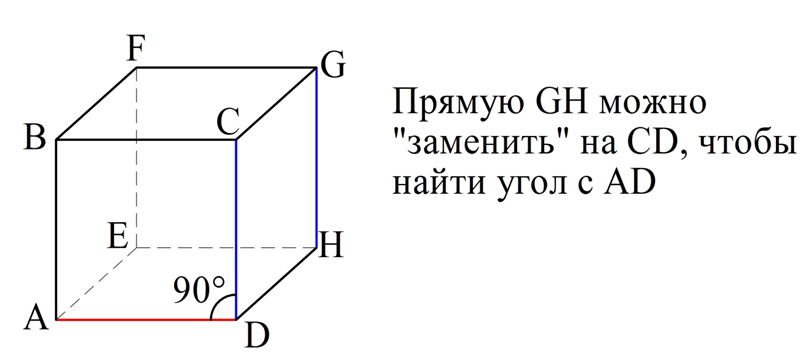
а) AD и GH. Заметим, что GH||СD, ведь это противоположные стороны квадрата СDHG, поэтому мы можем определить угол между AD и CD. Другими словами, мы просто заменяем в задаче GH на CD, так как эти отрезки параллельны. Так как отрезки AD и CD в свою очередь являются уже смежными сторонами в квадрате АВСD, то ∠ADC, который нам надо найти, составляет 90°.
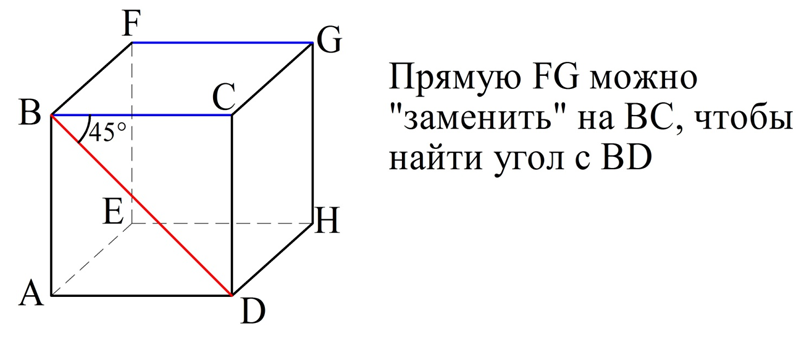
б) BD и FG. Здесь уже уместно заменить FG на ВС. Это можно сделать, ведь FG||ВС (это стороны квадрата). Тогда нам необходимо вычислить ∠СВD. Он составляет 45°, ведь диагональ квадрата делит его угол пополам.
в) BD и AF. Здесь есть смысл AF заменить на GD. Но для этого надо сначала показать, что AF||DG.Рассмотрим отрезки AD и FG. Каждый из них параллелен ВС (по свойству квадратов ABCD и ВСGH). Значит, по свойству транзитивности AD||FG, то есть эти отрезки располагаются в одной плос-ти. Тогда AFGD – плоский четырехугольник.
Заметим, что отрезки AD и FG ещё и одинаковы, так каждый из них равен ВС (вообще в кубе все ребра одинаковы). Получается, что в четырехугольнике AFGD стороны AD и FG одинаковы и параллельны, а потому AFGD – параллелограмм, по одному из его признаков. Отсюда и вытекает, что AF||DG.
Мы поняли, искомый нами угол между прямыми равен∠BDG. Как его вычислить? Для этого надо рассмотреть ∆BDG. Можно заметить, что он равносторонний. Действительно, отрезки BG, GD и BD – это диагонали в равных квадратах ВСGH, СDHG, АВСD, поэтому и сами эти диагонали также одинаковы. В любом равностороннем треугольнике все углы составляют по 60°, поэтому и ∠BDG равен этому же значению, то есть 60°.

Ответ: а) 90°; б) 45°; в) 60°.
Задание (стереометрическая задача из ЕГЭ). Точки А, В, С и D в пространстве располагаются так, что расстояния между любыми двумя из этих точек одинаковы. Можно доказать (попробуйте сделать это самостоятельно), что такая ситуация возможна лишь в случае, когда точки не располагаются в одной плос-ти. М – середина ВС, а L – середина АВ. Найдите косинус угла между прямыми МD и CL.
Решение. Из условия вытекает, что ∆АВС, ∆ВСD, ∆ABD – равносторонние и притом равные друг другу. Проведем в ∆АВС отрезок такой отрезок MF, что MF||СL. Тогда нам необходимо вычислить ∠DMF (точнее, его косинус). Это можно сделать, используя теорему косинусов применительно к ∆MDF, но для этого сперва надо найти все стороны в этом треугольнике:
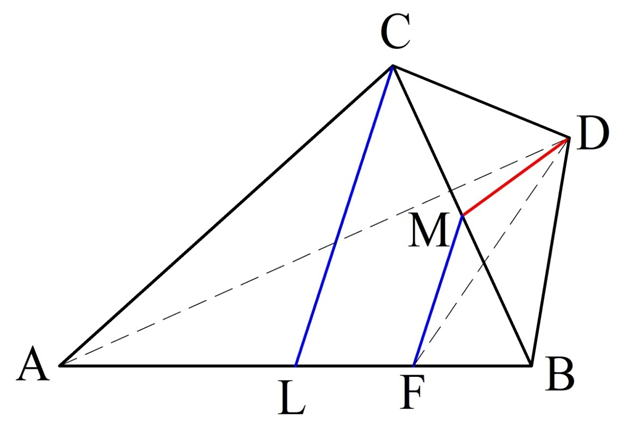
Для удобства обозначим длину отрезков АВ, ВС, АС, BD, AD и CD буквой R. Так как L– середина АВ, то CL– медиана в ∆АВС. Но в равностороннем треугольнике она одновременно будет и высотой. Тогда ∆АСL – прямоугольный. Запишем для него теорему Пифагора:
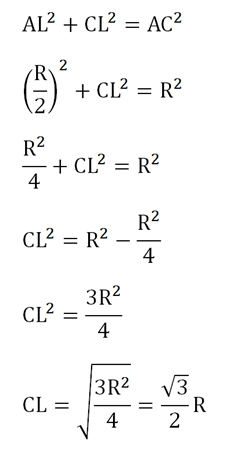
Аналогичным образом легко определить, что длина медианы DМ в ∆ВСD равна этому же значению:
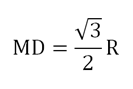
Теперь исследуем ∆ВСL. Так как MF||CL и М – середина ВС, то MF оказывается средней линией в ∆ВСL. Значит, ее длина вдвое меньше, чем у СL:
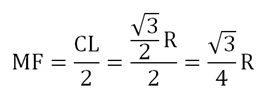
Также из того факта, что МF – средняя линия, вытекает то, что F – середина LВ. Тогда можно вычислить FB:
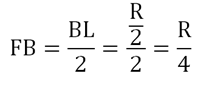
Далее обратим внимание на ∆ВFD. ∠В в нем составляет 60°, ведь это одновременно и угол в равностороннем ∆АВD. Стороны FB и BD нам известны, а потому с помощью теоремы косинусов можно вычислить и FD:
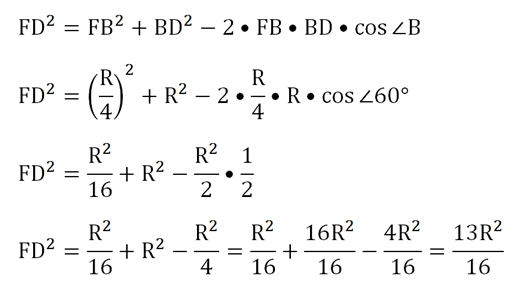
Теперь можно составить и для ∆МDF уравнение на основе теореме косинуса, из которого удастся выяснить интересующий нас косинус ∠DMF:

В ходе сегодняшнего урока мы познакомились с новым понятием – скрещивающимися прямыми. Также мы узнали, как вычислять угол между ними. Подобные задачи могут встречаться и на ЕГЭ.
ВОПРОСЫ И ЗАДАНИЯ
Сколько плос-тей можно провести через две скрещивающиеся прямые?
1) Одну 2) Две 3) Бесконечно много 4) Ни одной
Если MНР = 120°, то угол между прямыми МН и НР составляет…
1) 120° 2) 60° 3) 30° 4) 90°
Если прямые MН и РК скрещивающиеся, то прямые НР и МК…
1) Также скрещивающиеся 2) Параллельные 3) Пересекающиеся 4) Касательные
Максимальное значение угла между прямыми составляет…
1) 360° 2) 45° 3) 90° 4) 180°



