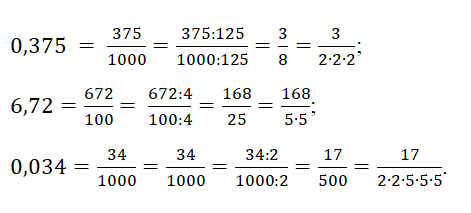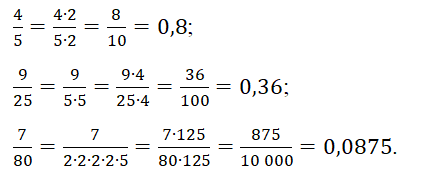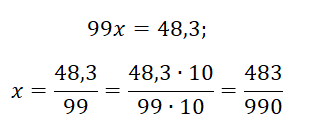План урока:

Натуральные числа

Простые и составные числа

Отрицательные и целые числа

Рациональные числа

Иррациональные и действительные числа

Натуральные числа

Ещё в далекие доисторические времена человек освоил такую математическую операцию, как счет. Можно было подсчитать количество соплеменников в племени или животных в стае, на которых велась охота. При этом человек ещё не осознавал понятие числа как некое отвлеченное понятие. Анализ языков народов, находящихся на самых низких стадиях развития, показывает, что они в словосочетаниях «три змеи», «три палки», «три камня» используют разные слова для числа 3. Однако со временем человек осознал, что количество предметов можно определять числом, которое не будет зависеть от природы подсчитываемых объектов. Числа, используемые для счета, сегодня называют натуральными числами. Долгое время человечество не знало никаких других чисел.

В качестве примера можно привести следующие натуральные числа: 1, 8, 10, 1000, 64141 и т.п. Если можно представить, что в каком-то множестве содержится N элементов, то N будет натуральным числом.

Вообще все натуральные числа являются частью так называемого натурального ряда чисел. Начинается этот ряд с единицы, а каждое следующее число больше предыдущего на 1.

Таким образом, можно дать ещё одно определение натуральных чисел – это числа, входящие в натуральный ряд. Традиционно ноль не является натуральным числом, ведь при подсчете предметов счет начинают с единицы. Такой подход используется в большинстве российских источников. Однако стоит отметить, что иногда в зарубежной литературе всё же предпочитают начинать натуральный ряд не с единицы, а с нуля. В этом случае 0 становится натуральным числом. Это деление весьма условно. Для обозначения множества натуральных чисел используется буква N. Очевидно, что натуральных чисел существует бесконечно много, а потому не существует наибольшего натурального числа.

Любые два натуральных числа можно складывать друг с другом и перемножать, при этом в результате будет снова получаться натуральное число. При вычитании может получиться ноль или отрицательное число, а при делении – дробное.

Простые и составные числа

Все натуральные числа можно разбить на три группы:

• простые числа;
• единица;
• составные числа.

Единицу традиционно не считают ни простым, ни составным числом. Составным же называют натуральное число, делящееся не только на единицу и себя. Можно дать и другие определения, основанные на количестве делителей у числа. Так, единица имеет ровно 1 делитель. У простого числа всегда ровно 2 делителя, а у составного – 3 и более.

В качестве примера простых чисел можно привести: 2, 3, 5, 7, 31, 101, 163. Примерами составных чисел являются:

• 4 (делится на 2);
• 6 (делится на 2 и 3);
• 8 (делится на 2 и 4);
• 33 (делится на 3 и 11)
• 50 (делится на 2, 5, 10, 25).

Среди делителей составного числа могут быть как другие составные, так и простые числа. Например, 50 имеет простые делители 2 и 5 и составные 10 и 25.

Заметим, что если число n делится на m, а m в свою очередь делится на k, то и n делится на k. Так, 45 делится на 9, а 9 делится на 3. Значит, и 45 делится на 3. Из этого свойства чисел вытекает следующее утверждение:

Любое составное число имеет хотя бы один простой делитель, причем им обязательно будет наименьший из всех делителей числа. Докажем это. Пусть число H – составное, и имеет наименьший делитель F. Предположим, что F – составное число. Тогда у него есть делитель L, который меньше его. Но тогда L должен быть делителем и для H. Так как L<F, и L – делитель для H, то F оказывается не наименьшим делителем. Получили противоречие, следовательно, исходное предположение (что F – составное число) неверно. Значит, F – простое число.

Получается, что для проверки простоты числа достаточно проверить, что оно не делится ни на одно простое число, меньшее себя, кроме единицы.

Существует специальный алгоритм, известный как решето Эратосфена. С его помощью можно найти все простые числа вплоть до заданного. Пусть надо найти все простые числа, не большие 30. Запишем их в ряд или, для компактности, в виде таблицы:

Первое простое число – это 2. Выделим ее, а потом зачеркнем в списке чисел все те, которые делятся на 2 (зачеркнуты синим цветом):

Из незачеркнутых чисел (кроме 1) наименьшим является тройка. Это значит, что она является простым числом, ведь мы не нашли простых чисел, которые меньше ее и которые являются ее делителем. Выделим тройку и также зачеркнем в табличке все числа, кратные ей и не зачеркнутые ранее (зачеркнуты красным цветом):

Так как четверка уже зачеркнута, то следующим простым числом оказывается пятерка. Снова выделим ее и зачеркнем числа, кратные 5 (зачеркнуто зеленым цветом, число 25):

Продолжая процесс, можно вычеркнуть в таблице все составные числа, а останутся только простые. В рассматриваемом примере уже не удастся вычеркнуть ни одно составное число, так как они были вычеркнуты ранее:

Есть данные, что понятие простых чисел было известно во времена Древнего Египта или даже в дописьменный период истории, однако только в древнегреческих источниках содержатся первые теоремы о них. Евклид доказал, что простых чисел бесконечно много.

Действительно, предположим, что существует некий конечный список из n простых чисел:

Перемножим их все, а после добавим единицу:

Q = p1 * p2 * p3 * ... * pn + 1

Получившееся число Q будет давать при делении на числа остаток, равный единице. То есть Q не будет делиться ни на одно число из первоначального списка.

Например, если есть список из простых чисел 2, 3, 5, 7, то число Q будет равно:

Q = 2•3•5•7 + 1 = 210+1 = 211.

Число 211 не делится на 2, 3, 5 и 7.

Получается, что либо число Q– простое (как раз таким является число 211), либо существует простое число, не входящее в первоначальный список (так как все составные числа имеют хоть один простой делитель). Значит, не существует такого списка, который включал бы все простые числа. Следовательно, простых чисел бесконечно много

Существует важное утверждение, которое называют основной теоремой арифметики:

Проиллюстрируем это на примере. Возьмем число 220. Оно является составным, так как делится на 2. Поэтому его можно представить в виде:

220 = 2•110.

В свою очередь число 110 также является составным, так как делится на 2. Значит, его можно разложить:

110 = 2•55.

Тогда и изначальное число 220 можно представить в виде:

220 = 2•110 = 2•2•55.

Продолжая раскладывать множители, можно получить запись:

220 = 2•110 = 2•2•55 = 2•2•5•11.

Теперь в правой части стоят только простые числа 2 (два раза), 5 и 11. Разложение можно представить в виде рисунка:

Основная теорема арифметики утверждает, что таким образом на простые множители можно разложить любое составное число. Действительно, если число составное, то его можно разложить на произведение двух множителей. Если один из них окажется составным, то его снова можно разложить на множители, и так до тех пор, пока в произведении не останутся исключительно простые числа. Таким образом, простые числа являются своеобразными «кирпичиками», из которых можно составить все натуральные числа.

С простыми числами связано множество интересных фактов. Например, существует гипотеза, что любое четное число, большее 2, можно представить как сумму двух простых чисел. Например:

4 = 2+2;

6 = 3+3;

8 = 3+5;

10 = 3+7;

100 = 43+57;

500 = 13+487;

1000 = 89+911.

Это утверждение носит название «гипотеза Гольдбаха». Хотя звучит она очень просто, а сформулирована была в 1742 году, на самом деле до сих пор (на 2019 год) никому не удалось ни доказать, ни опровергнуть это утверждение.

Отрицательные и целые числа

Периодически при решении разнообразных задач оказывалось, что одних натуральных чисел недостаточно для нужд человека. Так, если человек заработал за день 5 монеток, но потратил на еду 6, то насколько увеличился его капитал? Для этого надо вычесть из пяти шесть, то есть из меньшего большее. В Античности подобные операции над числами не допускались. Примерно в VI–VIII веке в Китае, а потом и Индии математики все же стали использовать отрицательные числа, воспринимая их как символ «долга». Выяснилось, что они очень удобны и помогают существенно упростить вычисления.

В Европе первые упоминания об отрицательных числах относятся к XIII веку, однако долгое время они не признавались математиками и считались абсурдными. Лишь в XVII веке, когда произошло развитие аналитической геометрии и появилось наглядное изображение отрицательных чисел с помощью числовой, или координатной оси, отрицательные числа получили всеобщее признание. Однако лишь в XIX веке была создана достаточно строгая теория отрицательных чисел.

На числовой оси отрицательные числа располагаются левее нуля, в то время как натуральные (положительные) правее:

Добавление к числу единицы означает перемещение на одну позицию вправо, а вычитание – на одну позицию влево. Так, если из 3 надо вычесть 6, то это значит, что от точки 3 надо сделать влево шесть шагов:

В результате получается, что 3 – 6 = – 3.

Если два числа в сумме дают ноль, то они называются противоположными. В своей записи они отличаются только знаком. Так, противоположны друг другу числа 5 и – 5, 10 и – 10, 25 и – 25. Считается, что ноль противоположен сам себе. Ноль, натуральные числа, а также числа, противоположные натуральным, образуют множество целых чисел.

Для обозначения множества целых чисел используется буква Z.

Рациональные числа

Пока человек использовал числа только для счета и сложения, ему вполне хватало натуральных чисел. Однако уже во время появления первых цивилизаций возникли задачи, связанные с делением. Например, определение площадей участков. Выяснилось, что для расчетов необходимо ввести особые, рациональные числа, то есть дроби. Например, если один пирог разрезать на две равные части, то получится две половины. Если же далее разделить одну из половин еще на две части, то каждая из них будет составлять четверть от изначального пирога.

В качестве примера рациональных чисел можно привести дроби:

• 2/3;
• 5/7;
• – 9/19;
• 23/15;
• 8/1.

Стоит заметить, что все целые числа также являются рациональными. Чтобы их представить в виде дроби, надо само число записать в числителе, а в знаменателе поставить единицу:

5 = 5/1;

18 = 18/1;

– 4 = – 4/1;

– 152 = – 152/1;

0 = 0/1.

В определении рационального числа не случайно указано, что в числителе должно находиться целое число, а в знаменателе – натуральное. Это связано с делением на ноль. Сам ноль, который является целым числом, может стоять в числителе. Однако деление на него запрещено, поэтому и указано, что в знаменателе должно стоять только натуральное число. Ноль не считается натуральным числом, а потому не может быть в знаменателе.

Напомним, почему деление на ноль не допускается. Операция деления определяется как операция, обратная умножению. Например, поделить 42 на 6 – это значит найти такое число x, для которого верно равенство:

6•x = 42.

Очевидно это число 7. Поэтому 42:6 = 7.

Теперь рассмотрим деление нуля. Например, поделим его на 5. Чему должен равняться x, чтобы выполнялось равенство

5•x = 0?

Такое значение x существует и равняется нулю:

5•0 = 0.

Значит, 0:5 = 0. Аналогично можно убедиться, что при делении нуля на любое число будет получаться ноль.

Теперь рассмотри деление на ноль. Поделим число 5 на него. В результате получим такое значение x, при котором будет выполняться равенство

0•x = 5?

Однако при любом значении x левая часть будет равна нулю, а потому искомого нами значения x просто не существует. Поэтому невозможно указать результат деления числа на ноль. Из-за этого считается, что эта операция не имеет смысла.

Те рациональные числа, которые не являются целыми, называют дробными.

Все множества рациональных чисел традиционно обозначают буквой Q. Правила вычислений с помощью дробей уже изучались в ранних классах, поэтому кратко напомним их.

Знаменатель и числитель дроби можно умножить на одно и тоже число (кроме нуля), и тогда дробь не изменится. Это правило известно как основное свойство дроби:

v*q=p

Обе части равенства можно умножить на число n:

v*q*n=p*n

v*(q*n)=(p*n)

Теперь поделим обе части на произведение q•n:

v = (p*n)/(q*n)

Приведем пример с числами. Известно, что 5 = 20/4. Это значит, что

5•4 = 20.

Умножим обе части, например, на 3:

5•4•3 = 20•3.

5•12 = 60.

По определению деления получаем, что 5 = 60/12, или

Получается, что одну и ту же дробь можно записать по-разному. Если числитель и знаменатель имеют общий делитель (за исключением единицы), то есть их можно сократить, то дробь называют сократимой. В противном же случае она именуется несократимой. Так, дробь 4/6 сократимая, так как и 4, и 6 делятся на 2. А вот дробь 2/3 несократима, так как у числителя и знаменателя нет общих делителей. Любую сократимую дробь можно привести к несократимой.

Если при записи дроби в явном виде используется дробная черта, то такую запись называют обыкновенной дробью. Однако на практике очень часто используют другое представление рациональных чисел, в виде десятичной дроби. Так называют дроби, в знаменателе которых стоит либо число 10, 100, 1000 или любая другая степень числа 10. Их можно записывать без использования дробной черты:

3/10 = 0,3;

8/100 = 0,08;

12345/1 000 = 12,345;

753/100 000 = 0,00753.

Любую десятичную дробь всегда можно записать в виде обыкновенной. При этом можно заметить, что если десятичную дробь записать в виде обыкновенной, а потом, сокращая числитель и знаменатель, получить несократимую дробь, то в результате знаменатель всегда можно будет представить как произведение чисел 2 и 5.

Это свойство связано с тем, что число 10 в любой степени – это произведение двоек и пятерок:

10 = 2•5;

100 = 10•10 = 2•5•2•5;

1000 =10•10•10 = 2•5•2•5•2•5.

При сокращении дроби мы «вычеркиваем» делители из числителя и знаменателя, а не добавляем их, поэтому в знаменателе так и останутся только двойки и тройки:

Получается, что любой конечной десятичной дроби соответствует несократимая обыкновенная дробь, в знаменателе которой представим как произведение двоек пятерок. Следовательно, обратное действие, перевод несократимой обыкновенной дроби в десятичную, можно выполнить исключительно тогда, когда в знаменателе дроби находится произведение двоек и пятерок. Например:

А вот дроби 2/3, 4/7, 10/13 невозможно представить в виде конечной десятичной дроби, так как их знаменатели 3, 7 и 13 нельзя представить как произведение двоек и пятерок.

Однако существуют и бесконечные десятичные дроби. В качестве примера можно привести числа:

1,3333333… = 1,(3);

45,38555555… = 45,38(5);

187,696969696969… = 187,(69).

Запись в скобках называется периодом. Период – это набор цифр, который повторяется в записи десятичного числа бесконечное количество раз, например, запись 0,5684 (9723) означает дробь 0,56849723972397239723…, где набор цифр 9723 повторяется бесконечно:

Десятичная дробь, имеющая период, называется периодической десятичной дробью. Можно представить и непериодические дроби, например:

• 0,12345678910111213141516… (здесь после запятой последовательно записываются все натуральные числа, начиная с единицы);
• 0,10100100010001000001… (здесь в дробной части только нули и единицы, причем количество нулей, отделяющих соседние единицы, с каждым разом увеличивается).

Между периодическими дробями и рациональными числами существует глубокая связь:

Чтобы произвести разложение обыкновенной дроби в бесконечную периодическую, следует просто выполнить ее деление столбиком. Покажем это на примере дроби 15/11:

На первой стадии деления столбиком получаем 1 с остатком 4. Далее дописываем к четверке ноль и продолжаем деление, записывая получаемые цифры уже после запятой:

Обратим внимание, что после записи чисел 3 и 6 мы снова получили в остатке 4 (выделено красным квадратом). Если продолжить деление, то вскоре мы снова получим 4 в остатке:

Таким образом, деление можно продолжать бесконечно, постоянно сталкиваясь с одними и теми же остатками. В периоде дроби получаем числа 3 и 6:

15/11 = 1,36363636… = 1,(36).

Несколько сложнее выполнить обратное преобразование, то есть получить обыкновенную дробь из периодической. Для этого надо составить уравнение. Покажем это на примере дроби 0,4(87). Примем ее за x:

x = 0.4(87) = 0.487878787...

В периоде две цифры, поэтому умножим уравнение на 100. Если бы в периоде была одна цифра, то умножать уравнение следовало бы на 10, а если 3 – то на тысячу. Сколько цифр содержится в периоде, столько и нулей должно быть после единицы у числа, на которое мы умножаем уравнение:

100*x = 100*0.4(87) = 48.7878787... = 48.7(87)

В правой части мы просто передвинули запятую на два разряда вправо. Теперь вычтем из второго уравнения первое:

100*x - x = 48.7(87) - 0.4(87)

Если в правой части произвести вычитание столбиком, то период исчезнет:

В результате получаем уравнение:

Итак, исходная дробь равна 483/990. Можно проверить себя и на калькуляторе поделить эти числа. В результате получится 0,487878787…

Иррациональные и действительные числа

Долгое время дробей было достаточно человечеству для любых расчетов. Древние греки полагали, что любое отношение величин, которое может встретиться в реальном мире, будет выражаться какой-нибудь дробью. Однако это не так. Один из учеников Пифагора, Гиппас, пытался найти соотношение между стороной квадрата и его диагональю. В результате он осознал, что такой дроби просто не существует.

Это соотношение равно квадратному корню из 2 (что доказывается в курсе геометрии), которое обозначается как 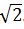. Это такое число, которое при умножении на само себя дает 2. Докажем, что оно не может быть выражено несократимой дробью.

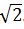
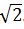
При этом она равна дроби 2/1. Следовательно, b*b = 1 , а a*a = 2. Однако не существует такого натурального числа a, которое при умножении на себя дает 2. Получается противоречие, значит,  нельзя представить в виде дроби. Математики говорят, что  является иррациональным числом. Аналогичным образом можно доказать иррациональность квадратного корня из любого натурального числа, не являющимся квадратом другого натурального числа.

Исторически именно 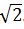 был первым иррациональным числом, открытым человечеством. Его значение примерно равно 1,414213562. Способы его вычисления будут освещены позже. Заметим лишь, что у этого числа нельзя найти периода в его десятичной записи.

Вообще любое иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби. Это значит, что в числах после запятой не будет никакого периода. Чуть раньше мы уже приводили два примера иррациональных чисел:

• 0,12345678910111213141516…;
• 0,10100100010001000001….

Ещё одним иррациональным числом является π, которое равно отношению длины окружности к ее диаметру и примерно равно 3,1415926…

Для обозначения множества иррациональных чисел используется буква I.

Рациональные и иррациональные числа вместе образуют множество действительных чисел, обозначаемое буквой R. Иногда их также называют вещественными числами.

Слово «вещественное» указывает на физический смысл этого понятия. Любой результат измерения какой-либо величины (длины, площади, объема, массы и т. д.) является вещественным числом.

Важно, что на числовой прямой, или координатной оси, каждой точке в соответствие можно поставить действительное число, и наоборот, каждому действительному числу соответствует единственная точка на числовой прямой. В качестве примера показаны числа π и 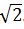 на числовой прямой:

Таким образом, можно составить следующую классификацию чисел, используемых в математике:

Все числа, которые встретятся в ходе изучения школьной программы математики и других наук, будут действительными. Однако стоит отметить, что в высшей математике, изучаемой в университете, будут изучаться и более сложные объекты, называемые комплексными числами.